Криволінійні інтеграли. Умова незалежності інтеграла від лінії інтегрування. Інтегрування повних диференціалів. Первісна функція, страница 2

лінії інтегрування рівносильно рівності нулю інтеграла (7.2) по будь-якому замкнутому контурі, що міститься цілком в області D. Доведемо спочатку достатність умови теореми для рівності нулю інтеграла по будь-якому замкнутому контурі. Візьмемо довільний замкнутий контур L*, що обмежує область D* і цілком лежачий усередині області D (рис. 8.1 а), і застосуємо до нього формулу Гріна: 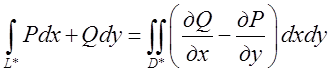 . Так як за умовою 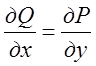(*), то подвійний інтеграл дорівнює нулю. Отже, дорівнює нулю і криволінійний інтеграл по контурі I.*, що і було потрібно довести.

Рис. 8.2.             Перейдемо до доказу необхідності умови теореми. Тому що нам дано тепер, що інтеграл (7.2) по л ю б о м у замкнутому контуру дорівнює нулю, тобто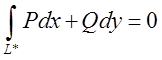 то, знову ж таки в силу формули Гріна, виходить, що дорівнює нулю і подвійний інтеграл: 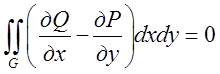, де G – будь-яка область, яка знаходиться  усередині області D. Допустимо, що рівність (*) не виконується. Візьмемо яку-небудь точку М,

у якій ця рівність порушується, і обчислимо в ній  різницю 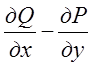. Допустимо, що ця різниця позитивна, тобто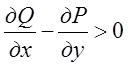. В силу припущення неперервності частинних похідних

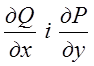звідси випливає, що різниця 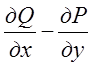 буде позитивна в деякій досить малій області G, що оточує точку М (рис. 8.2 б), тобто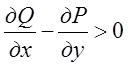 в усіх точках області G. Але тоді по властивості подвійних інтегралів, будемо мати ,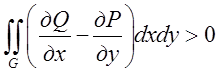

і ми прийшли до протиріччя з рівністю 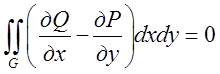. Це означає, що наше припущення про невиконання умови (*) було невірним, таким  чином ми довели, що 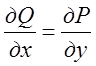у всій області D. Теорема повністю доведена.

Зверніть увагу на те, що вираз (*) своїм видом нагадує повний диференціал деякої функції . Як ми знаємо 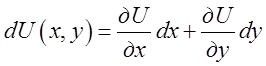 (**). Порівнюючи(*) і (**) бачимо, що (*) повним диференціалом буде тоді, коли 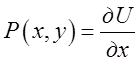, а

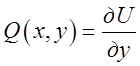.  Пригадуючи теорему про рівність змішаних частинних похідних другого порядку 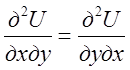, ми приходимо до думки: для того, щоб вираз (*) був повним диференціалом необхідне виконання рівності 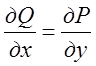. Запишемо це як

 Теорема II. Якщо функції  і їхні частинні  похідні неперервні в однозв'язній області Q  і в усіх її  точках виконується рівність 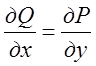, то вираз є повним диференціалом.

Доведення цієї теореми досить громіздке, його можна знайти в підручниках (наприклад [2. c 464]) і ми його приводити не будемо.

 Підводячм підсумки нашого дослідження, можна сказати таке:  якщо область D однозв'язна і функції  разом зі своїми частинними похідними неперервні в цій області, то всі чотири наступних твердження рівносильні, тобто якщо виконується одне з них, то виконуються і всі інші.

1. Криволінійний інтеграл 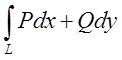, узятий по будь-якому замкнутому контуру, що цілком лежить в області D, дорівнює нулю.

2. Криволінійний інтеграл 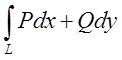 не залежить від лінії  інтегрування, що з'єднує дві дані точки.

3. Вираз   є повним диференціалом.

4. В усіх точках області D має місце рівність   .                                             

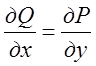Особливу роль грає четверте твердження, тому що саме з його допомогою звичайно перевіряється виконання всіх інших.

У просторовому випадку, так само як і в плоскому, існує тісний зв'язок між умовою незалежності інтеграла (7.2) від контуру інтегрування й умовою того, що підінтегральний вираз є повним диференціалом деякої функції трьох змінних. Щоб сформулювати відповідні теореми, уведемо визначення поверхово -однозв'язної області.

Тривимірна область  називається поверхово однозв'язною, якщо на будь-який простий кусочно-гладкий замкнутий контур, що належить області, можна натягнути плівку, що цілком лежить в області . По другому кажучи, будь-який замкнутий контур можна «стягти» у точку, залишаючись усередині області . Поверхово однозв'язними областями будуть, наприклад, багатогранник, куля, еліпсоїд і т.д. Такою ж областю буде порожня куля (кульове кільце). Необмеженими поверхово однозв'язковими областями будуть півпростір, зовнішність кулі, частина простору, укладена між двома паралельними площинами, і т.д.

Прикладом поверхово- неодносвязної області служить – тор («бублик»), тому що коло, описуване будь-якою точкою кола, обертанням якого був утворений тор, не може бути стягнуте в крапку, залишаючись усередині тора. Як і для плоских кривих, для просторових сформулюємо таких же чотири  твердження у вигляді

Теореми 3. Нехай функції  неперервні разом зі своїми частинними похідними в поверхово однозв'язній області . Тоді рівносильні наступні твердження:

1.Криволінійний інтеграл 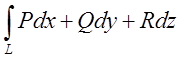, узятий по будь-якомузамкнутому контуру, що цілком лежить в області , дорівнює нулю.