Криволінійні інтеграли. Методи обчислення криволінійних інтегралів. Інтеграли по замкнутому контуру

Лекція 7

Криволінійні інтеграли

 7.1. Задачі, які приводять до поняття криволінійних інтегралів. Означення криволінійних інтегралів.

 7.2. Методи обчислення криволінійних інтегралів.

 7.3. Приклади.

 7.4. Інтеграли по замкнутому контуру.

 7.5. Формула Гріна.

 7.6. Питання самоконтролю.

Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.

Математичні факти з попередніх розділів, які використовуються в даній лекції.

1. Пригадайте, як знайти рівняння прямої лінії заданої координатами двох своїх  точок: 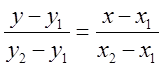. Це рівняння дуже легко звести до рівняння загального виду , або до виду рівняння у відрізках 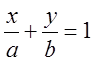. Будують пряму, визначивши дві її точки (найкраще точки перетину її з вісями координат). Перегляньте і згадайте ще раз вступ до лекції 4, де подано рівняння і графіки кривих.

2. Якщо маємо якийсь вектор  і  вісь  s  з напрямним вектором  та кут  між цією віссю і вектором  , то проекція вектора на вісь s обчислюється за формулою 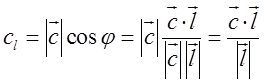. Якщо ж ці вектори задані своїми координатами   і  , то їх скалярний добуток буде .

3. Якщо дуга, зображена на рисунку,  задана рівняннями  

  то згідно теореми Піфагора 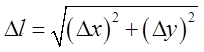. Якщо , то в звязку з неперервністю функції, якою задана крива і , а значить і і ми маємо право записати 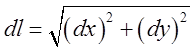=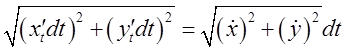. А якщо крива задана рівнянням , то диференціал дуги  

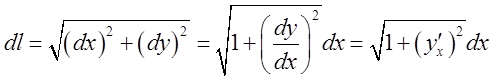
4. Якщо маємо рівняння кривої в парамнтричному виді , а треба перейти до рівнянняому виді, то, розвязуючи систему 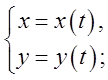 виключають t.

7.1.Задачі, які приводять до поняття криволінійних інтегралів. Означення криволінійних інтегралів

Задача 1.Обчислити роботу силового поля  при русі  матеріальної точки масою т під дією сили цього поля вздовж  деякої лінії L від точки В до точки С.

Розв’язання цієї задачі було б під силу школяреві  старшокласнику коли б сила, яка діє на точку, мала постійне значення і напрямок, а  точка від В до С рухалась вздовж прямої лінії. В цьому випадку робота дорівнювала б скалярному добутку вектора сили на вектор переміщення  .

Але ж у нас і сила і напрям руху змінні величини і якщо ми вектор діючої сили на масу т в точці В скалярно перемножимо на вектор переміщення, то одержимо значення роботи дуже приблизне. Ближчим до істинного значення була б сума робіт вздовж ламаної лінії , де точки  лежать на кривій L. Визначаючи роботу, и скористаємось тими

                 Рис. 7.1                                ідеями, які привели нас           до поняття одно- двох- і трьохвимірного інтеграла.  Замінимо кожен з відрізків кривої  відповідним йому  вектором  . Їх буде п штук. Ці вектори будуть мати малу довжину (в подальшому вона у нас буде прямувати до 0), а тому вважатимемо, що сила, яка діє на точку при її русі вздовж вектора   буде постійною і дорівнює =  . Довжина   нехай буде , тобто  і =. При цьому елементарна робота на цій ланці ламаної буде . Або

 . Щоб знайти всю роботу, треба знайти суму 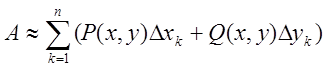. Ця сума називається інтегральною сумою по лінії L і  приблизно виражає шукану роботу. Точне значення ми одержимо тоді, коли довжини ланок ламаної будемо нескінченно зменшувати, (при цьому кількість ланок в ламаній буде нескінченно збільшуватись) тобто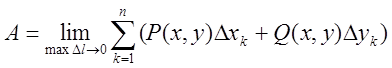                  (7.1)

Границя  інтегральної суми (7.1) при прямуванні до 0 довжини найбільшої з ланок ламаної, кутові точки якої лежать на кривій L, називається криволінійним інтегралом по лінії L, тобто 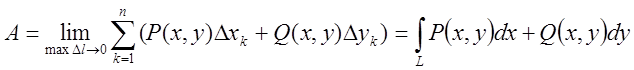            (7.2)

            Такий інтеграл ще називають криволінійним інтегралом за координатами. Йому дали  назву інтеграл другого типу.  Звернім увагу на те, що коли ми змінимо напрям руху точки на протилежний, то на протилежні зміняться знаки в . А значить на протилежний зміниться знак суми, інтеграла і роботи

Задача 2. Знайти масу дільниці  плоскої кривої L від точки В до точки С, якщо лінійна густина речовини кривої є функція    .