 (*)
(*)
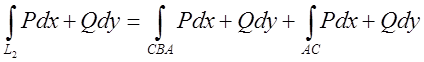 (**)
(**)
Інтеграли по СА і АС беруться по одній і тій же лінії але в протилежних напрямках, а тому вони рівні за абсолютною величиною, але протилежні за знаком і їх сума дорівнює нулеві. Тому коли ми складемо (*) і (**) то одержимо
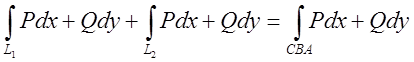 +
+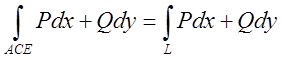 (7.10)
(7.10)
Теорема виконується і в тому випадку коли область D розбити на яку завгодно скінченну кількість областей. Для інтегралів по замкнутому контуру застосовують позначення
![]() , або
, або 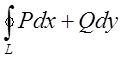 ,
вказуючи напрям обходу контура.
,
вказуючи напрям обходу контура.
7.5.Формула Гріна.
Теорема. Якщо функції P(x,y) і Q(x,y) неперервні разом зі своїми частинними похідними в замкнутій обмеженій області D, то має місце формула
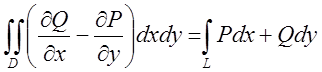 (7.11)
(7.11)
Доведення.
|
|
В
площині ХОУ візьмемо область D ,
обмежену лінією L. Причому область D така, що прямі,
паралельні координатним осям, перетинають її границю L не більше ніж в
двох точках рис.7.5. В основі доведення лежить перетворення подвійного
інтегралу через криволінійний 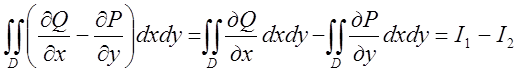 .
.
Довівши,
що ![]() дорівнює криволінійному
інтегралу Рис. 7.5 по L ми доведемо
(7.11). Перетворимо інтеграл
дорівнює криволінійному
інтегралу Рис. 7.5 по L ми доведемо
(7.11). Перетворимо інтеграл ![]() .
.
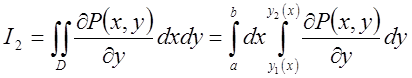 ={внутрішній інтеграл береться від диференціала, а
тому
={внутрішній інтеграл береться від диференціала, а
тому 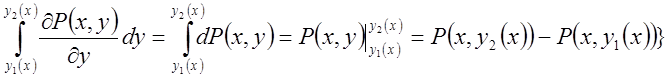 =
=
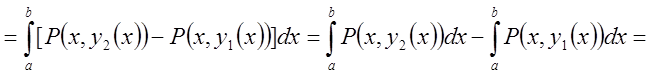 {в другому інтегралі поміняємо границі
інтегрування, а це призведе до зміни його знаку} =
{в другому інтегралі поміняємо границі
інтегрування, а це призведе до зміни його знаку} =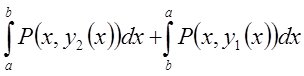 .
Згідно з формулою (7.5) обчислення криволінійних інтегралів, ці два інтеграли є
криволінійні інтеграли
.
Згідно з формулою (7.5) обчислення криволінійних інтегралів, ці два інтеграли є
криволінійні інтеграли 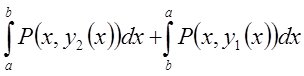 =
=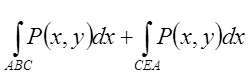 . Контур L(ABCEA) обходить область D у від’ємному напрямку, а тому
. Контур L(ABCEA) обходить область D у від’ємному напрямку, а тому
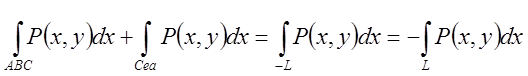 . (*)
. (*)
Аналогічні
міркування приводять нас до того, що 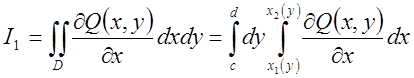 =
=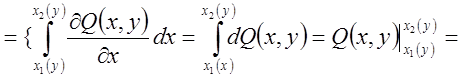
![]() }=
}=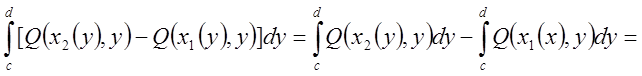
=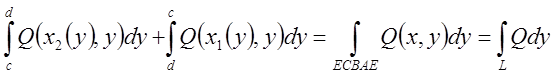 (**)
(**)
Замінимо
подвійні інтеграли в (7.11) знайденими (*) і (**) одержимо 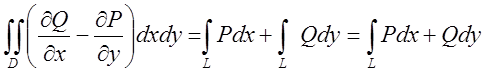 , що і треба було довести.
, що і треба було довести.
Доведення формули Гріна для неправильної області ґрунтується на розбитті її на правильні області, доведенні справедливості формули Гріна для кожної з правильних областей, а потім, використовуючи властивості адитивності подвійного і криволінійного інтеграла знаходять суму інтегралів подвійних по областях, криволінійних по кривих, які ці області обмежують.
П.6. Обчислити 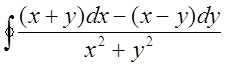 ,
де контуром є коло, рух проти часової стрілки.
,
де контуром є коло, рух проти часової стрілки.
Розв’язок. Контуром
візьмемо коло радіусом R. Тоді рівняння
контура : ![]() , причому, для того щоб точка обійшла весь
контур
, причому, для того щоб точка обійшла весь
контур ![]() повинно змінюватись від
повинно змінюватись від ![]() до
до ![]() , а тому
маємо
, а тому
маємо 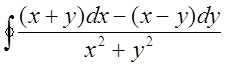 =
=
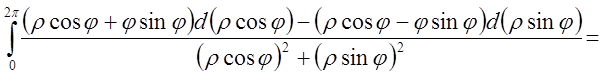
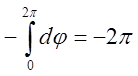 . Це є відповідь.
. Це є відповідь.
Зауваження. Застосовувати
формулу Гріна при розв’язувані цього прикладу ніяк не можна бо підінтегральні
функції P(x,y) i Q(x,y) в точці O(0,0), яка лежить в області D,
мають розрив другого роду, а значить подвійний інтеграл буде невластивим.
Перевіримо це. 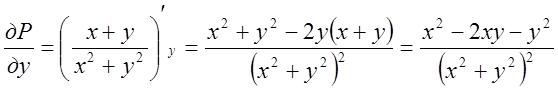
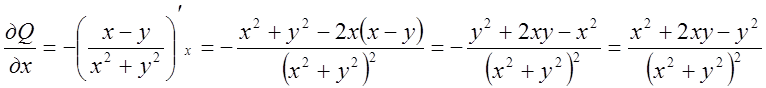 . Підставимо
. Підставимо
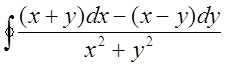 =
=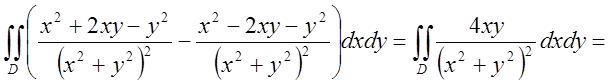
={якщо контуром є
коло радіусом R, і ми переходимо в полярну систему координат, то
границями для ![]() будуть:
будуть: ![]() ,
границями для
,
границями для ![]() будуть:
будуть: ![]() }=
}=
=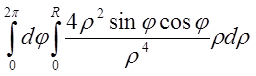 =
=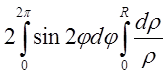 ={внутрішній
інтеграл дорівнює
={внутрішній
інтеграл дорівнює ![]() і в нижній границі одержуємо
і в нижній границі одержуємо ![]() }. Так, що застосовувати формулу Гріна можна лише
при виконанні умов теореми.
}. Так, що застосовувати формулу Гріна можна лише
при виконанні умов теореми.
Розв’яжіть самостійно
1.
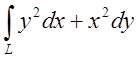 , де контуром є верхня половина еліпса x=a cost, y=b sint, рух по ходу годинної стрілки . Відп.
, де контуром є верхня половина еліпса x=a cost, y=b sint, рух по ходу годинної стрілки . Відп.  .
.
2.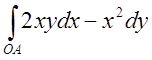 , узятий уздовж параболи,
віссю симетрії якої є вісь ОУ від точки О(0,0) до точки А(2,1). Відп.0.
, узятий уздовж параболи,
віссю симетрії якої є вісь ОУ від точки О(0,0) до точки А(2,1). Відп.0.
3.
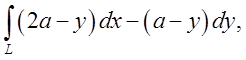 де L – перша арка
циклоїди
де L – перша арка
циклоїди ![]() . Відп.
. Відп.![]() .
.
4.
Застосовуючи формулу Гріна, перетворити криволінійний інтеграл 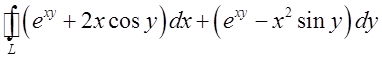 , взятий по замкнутому контуру з додатнім
напрямком обходу в подвійний інтеграл по області обмеженій цим контуром. Відп.
, взятий по замкнутому контуру з додатнім
напрямком обходу в подвійний інтеграл по області обмеженій цим контуром. Відп.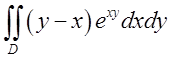 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.