Криволінійні інтеграли. Методи обчислення криволінійних інтегралів. Інтеграли по замкнутому контуру, страница 2

            Для розв’язку цієї задачі скористаємось тим же рисунком 7.1 і тією ж ідеєю розбиття кривої на відрізки ламаної і приблизного обчислення шуканої величини як суми її значень на кожному з відрізків, з наступним переходом до границі при . Вважаємо, що функція маси  на відрізку   є постійна величина. Нехай вона на ньому дорівнює . Можемо обчислити  масу цього відрізка  . Щоб знайти масу всієї ламаної треба знайти суму мас всіх відрізків Знайдена маса ламаної буде відрізнятись від маси кривої. 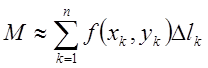. Це є інтегральна сума. Щоб  значення маси ламаної якомога точніше виражало значення маси кривої треба зменшувати . Ці значення співпадуть, коли ми перейдемо до границі при . Таким чином  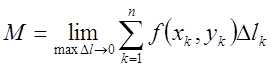                         (7.3)

 Кінечна границя цієї суми при  називається криволінійним інтегралом від функції  вздовж кривої L, тобто

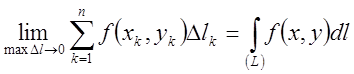            (7.4)

 Цей інтеграл дістав назву криволінійний інтеграл першого типу.

Таким чином, маса кривої 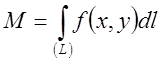. Звернімо увагу на те, що величина (7.4), на відміну від (7.2), не залежить від напрямку інтегрування, що підтверджується і фізичним змістом: величина  маси не залежить від методу її обчислення.

 7.2. Методи обчислення  криволінійних інтегралів

1.Криволінійний інтеграл другого типу зводиться до визначеного інтегралу у випадках.

а)Якщо крива L задана в явному рівнянням , то 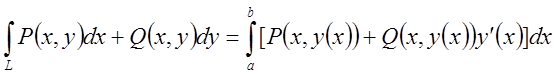                                                  (7.5) б)Якщо крива L задана параметричними рівнянням , то

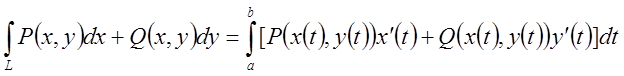                                      (7.6)

2.Криволінійний інтеграл першого типу зводиться до визначеного інтегралу у випадках.

а)Якщо крива L задана рівнянням , то  при  маємо 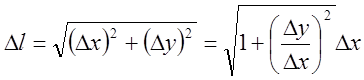 тому .

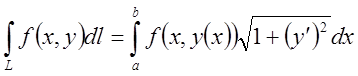                                                           (7.7)

б)Якщо крива L задана рівнянням , то  і при  одержимо

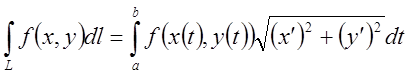                                                   (7.8)

Якщо крива інтегрування задана в трьохвимірному просторі , то формули обчислення інтегралів другого і першого типу мають вид

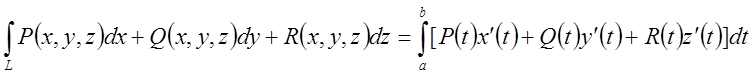                         (7.8а)

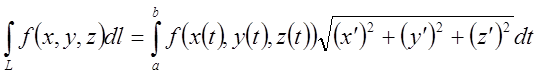                                                     (7.7а) 

                                                           7.3.Приклади

П.1.Обчислити 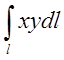, де l­- контур квадрата  

Запишемо рівняння сторін квадрата:

АВ:   x+y=a;    y=a-x;

BC:   y-x=a;     y=a+x;

CD:   x+y=-a;   y=-x-a;

AD:   x-y=a;      y=x-a;

Обчислимо ;

На AB y`=-1;     на BC  y`=1;    на СD   y`=-1;     на AD   y`=1.

Таким чином по всьому контуру  ;   

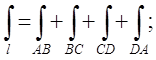
 Обчислимо окремо кожен з інтегралів.

;

 

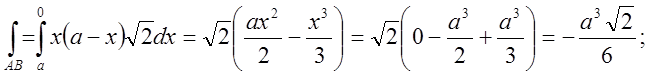
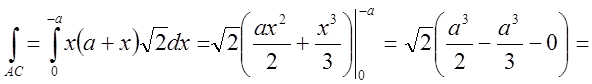
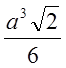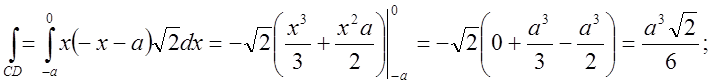
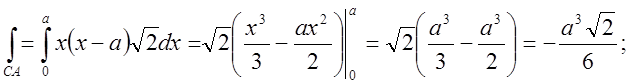
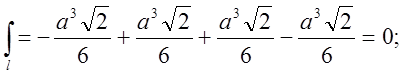   Відповідь:  0.

П.2.Обчислити 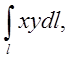  де l чверть еліпса  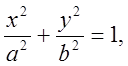яка лежить в першому квадранті.

Розв’язок.

  Представимо рівняння еліпса в параметричному виді x=a cos t,   y=b sin  t.

Очевидно, що для першої чверті границі зміни t будуть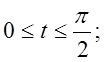   

                             Рис. 7.2 

 

  

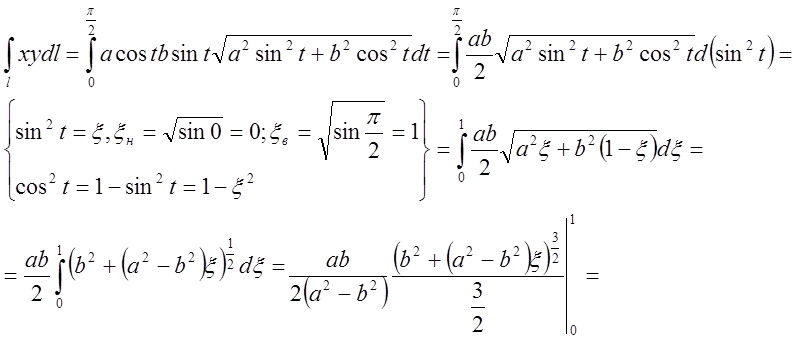
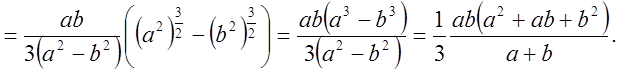
Велике значення в техніці має гвинтова лінія, як звернута на циліндр похила площина. Застосуємо її, як контур інтегрування. 

П.3. Обчислити 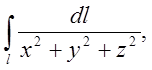   l – перший виток гвинтової лінії x=a cos t; y=a sin t; z=bt.                                                                                                                    

Розв’язок.

  Диференціал дуги у трьохвимірному просторі збереже такий же вид, як і  на площині, але добавиться ще координата z.      підставимо значення диференціалів

                       Рис. 7.3.                              

=

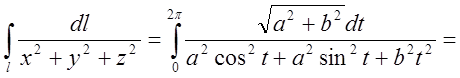
П.4. Знайти довжину дуги конічної гвинтової лінії     

від точки О(0;0;0;) до точки А

Розв’язок.

Знайдемо значення параметра  , яке відповідає положенню точки А.   тобто

 Знайдемо значення параметра  яке відповідає  положенню

точки О.   тобто  але ж . Звідси Це можливо лише при  

А тому

Підставимо  в  інтеграл ;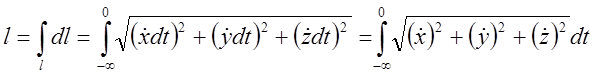

Обчислимо

;

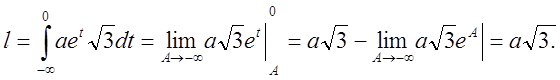
Відповідь:  

П.5. Обчислити 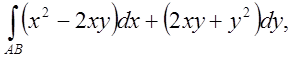де АВ – дуга параболи  від точки А(1;1) до точки В(2;4)

Розв’язок.

Підставимо в умову замість y те, чому він дорівнює коли ми проходимо вздовж кривої АВ, тобто . Ми одержимо звичайний одновимірний інтеграл з границями від  

до  

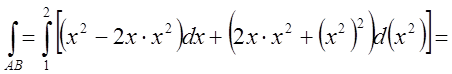
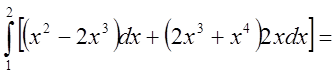
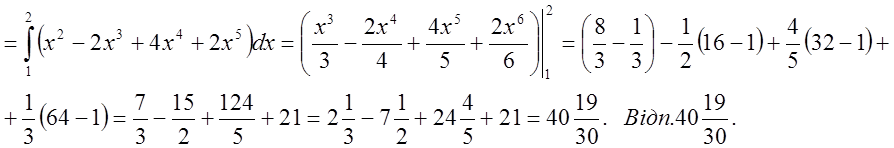
7.4. Інтеграли по замкнутому контуру

Розглянемо область D, обмежену замкнутою кривою L. Говорять, що при обході області D вздовж кривої L додатнім напрямком вважається той при якому область D під час обходу весь час залишається зліва. Відповідно від’ємним – коли область залишається справа. Тепер можемо записати 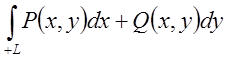  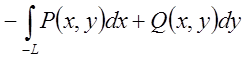 =               (7.9)

Теорема. Якщо область D, обмежену замкнутою лінією L, розбити на дві частини  то криволінійний інтеграл по всій лінії L буде дорівнювати сумі інтегралів, обчислених в тому ж напрямку по лініях , які обмежують області

Доведення. Нехай область D, як це зображено на рис. 7.4, обмежена замкнутою лінією , а області   відповідно             Рис.7.4.             лініями . Запишемо інтеграли взяті вздовж  в додатніх напрямках.