Гратчасті функції. Кінцеві різниці. Обчислення кінцевих різниць, додатків, первісних.
Приклад 1. Знайти рішення різницевого рівняння
![]()
з початковими умовами ![]() ,
, ![]() .
.
Розв’язання.
Застосуємо ![]() –
перетворення до рівняння
–
перетворення до рівняння
![]() ;
;
![]() ;
;
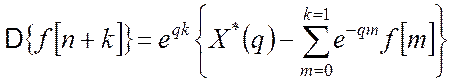 ;
;
![]() ;
;
![]() ;
;
![]() .
.
Підставимо отримані коефіцієнти до початкового рівняння:
![]() – рівняння операторного вигляду.
– рівняння операторного вигляду.
Звідси маємо:
![]() ;
;
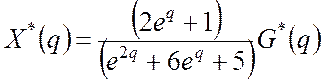 ;
;
або
![]() .
.
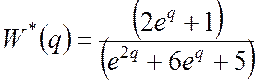 – передаточна функція системи.
– передаточна функція системи.
![]()
Нехай
![]() .
.
З теореми про обернене перетворення маємо:
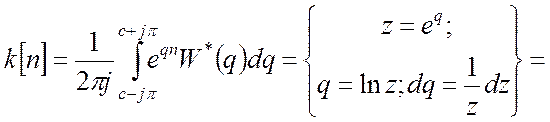
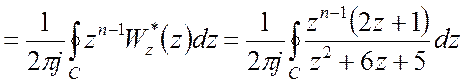 .
.
Згідно теореми про лишки отримуємо:
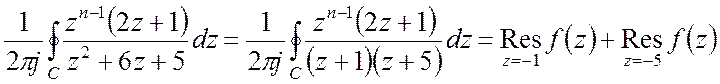 .
.
Звідси маємо:
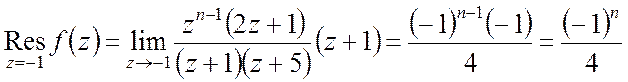 ;
;
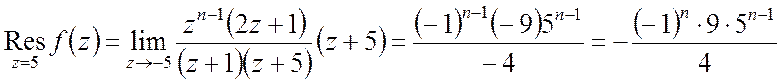 .
.
Таким чином
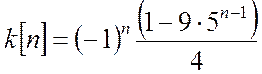 ;
;
![]() .
.
Тоді
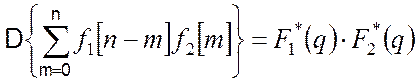 ;
;
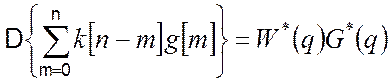 .
.
Звідси отримуємо відповідь:
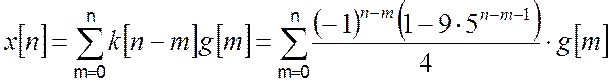 .
.
Відповідь: 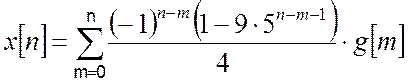 .
.
Приклад 2. Знайдіть кінцеві різниці таких функцій:
– ![]() ;
;
– ![]() ;
;
– ![]() ;
;
– ![]() ;
;
– ![]() ;
;
– ![]() .
.
Приклад 3. Знайти рішення різницевих рівнянь
–
![]()
з початковими умовами ![]() ,
, ![]() ;
;
– ![]()
з початковими умовами ![]() ,
, ![]() .
.
Рівняння імпульсних систем автоматичного регулювання.
Визначення реакції на типові діяння.
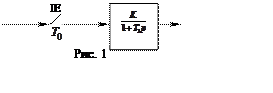 Приклад 1. На рис. 1 зображен імпульсний фільтр. Імпульсний елемент ІЕ генерує
прямокутні імпульси тривалістю
Приклад 1. На рис. 1 зображен імпульсний фільтр. Імпульсний елемент ІЕ генерує
прямокутні імпульси тривалістю![]() ,
де
,
де ![]() , а період повторення
, а період повторення ![]() . Передаточна функція неперервної частини
. Передаточна функція неперервної частини
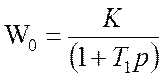 ,
,
де ![]() ,
а
,
а ![]() . Визначити передаточну функцію фільтра сумісно
з імпульсним елементом.
. Визначити передаточну функцію фільтра сумісно
з імпульсним елементом.
Розв’язання.
В даному випадку зображення Лапласу імпульсу, котрий генерується ІЕ при подачі на нього одиничного сигналу, буде дорівнювати
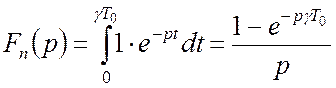 .
.
Приведена передаточна функція неперервної частини
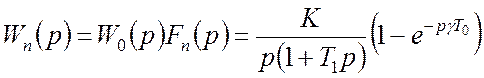 .
.
Звідси маємо
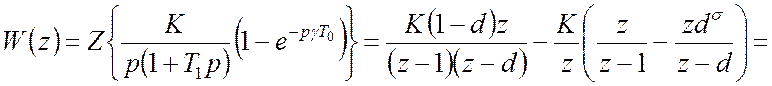
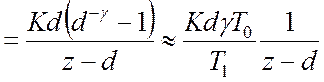 ,
,
де ![]() ,
а
,
а ![]() . Після підстановки числових значень маємо
. Після підстановки числових значень маємо
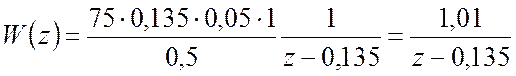 .
.
Приклад 2. Знайти частотну передаточну функцію імпульсного фільтру з прикладу 1 залежно від абсолютної псевдочастоти.
Розв’язання.
В передаточній функції прикладу 1 перейдемо до
![]() -перетворення за допомогою підстановки
-перетворення за допомогою підстановки 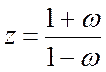 . В результаті маємо
. В результаті маємо
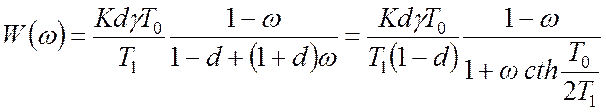 .
.
Перейдемо до абсолютної псевдочастоти 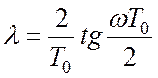 за допомогою підстановки
за допомогою підстановки 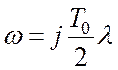 :
:
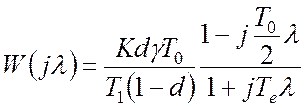 .
.
Тут введена еквівалентна постійна часу
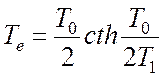 .
.
Підстановка числових значень дає ![]() . Передатна функція дорівнює
. Передатна функція дорівнює
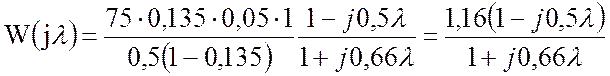 .
.
Приклад 3. Розв’язати приклад 1 за умовою, що відносна
тривалість імпульсу ![]() .
.
Розв’язання.
В цьому випадку згідно
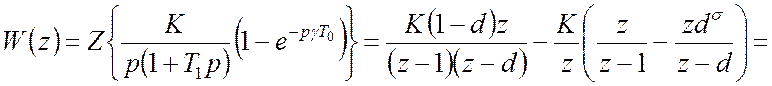
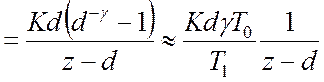 ,
,
маємо
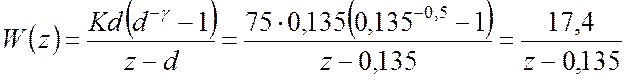 .
.
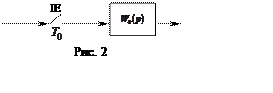 Приклад 4. Для імпульсного фільтру, зображеного на рис. 2, знайдіть логарифмічні
амплітудну та фазову характеристики. Передатна функція неперервної частини
Приклад 4. Для імпульсного фільтру, зображеного на рис. 2, знайдіть логарифмічні
амплітудну та фазову характеристики. Передатна функція неперервної частини
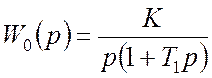 .
.
Початкові умови: ![]() ,
, ![]() ,
,
![]() та
та ![]() .
Вважати, що послідовність імпульсів на виході ІЕ може бути змінена на
послідовність
.
Вважати, що послідовність імпульсів на виході ІЕ може бути змінена на
послідовність ![]() -функцій.
-функцій.
Розв’язання.
Дискретна передатна функція імпульсного фільтру дорівнює
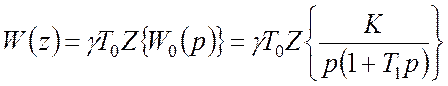 . (1)
. (1)
Тоді маємо
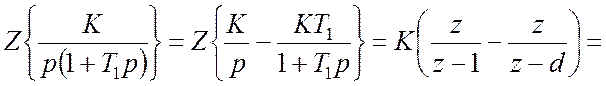
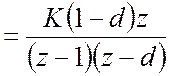 , (2)
, (2)
де ![]() .
Підставляючи (2) в (1), маємо
.
Підставляючи (2) в (1), маємо
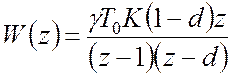 .
.
Використаємо підстановку 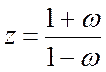 :
:
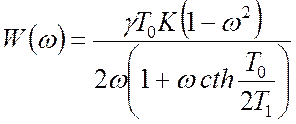 .
.
Перейдемо до абсолютної псевдочастоти
підстановкою 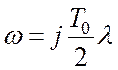
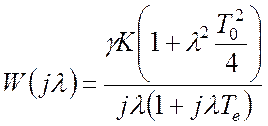 .
.
Тут 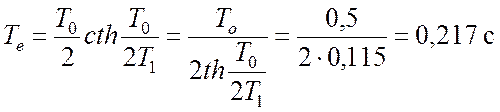 .
Підстановка числових значень дає
.
Підстановка числових значень дає
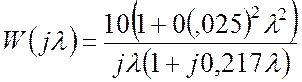 .
.
Логарифмічні амплітудна та фазова характеристики дорівнюють
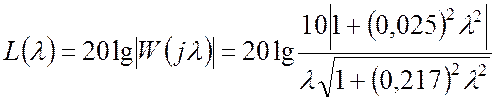 ,
,
![]() .
.
Дискретне перетворення Лапласа. Обчислення зображень.
Знаходження оригіналу по наданому зображенню.
Приклад 1. Знайти ![]() -перетрорення
для функції часу
-перетрорення
для функції часу
![]() ,
,
визначеної для ![]() .
Період дискретності
.
Період дискретності ![]() с.
Значення коефіцієнтів:
с.
Значення коефіцієнтів: ![]() ,
,
![]() та
та ![]() .
.
Розв’язання.
Маємо
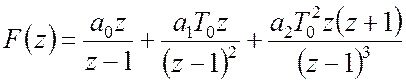 .
.
Підстановка числових значень дає
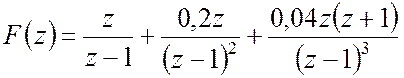 .
.
Приклад 2. Знайти ![]() -перетрорення
для функції часу, котра має таке зображення Лапласу
-перетрорення
для функції часу, котра має таке зображення Лапласу
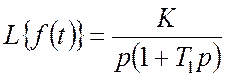 .
.
Розв’язання.
Розкладемо зображення на прості дроби
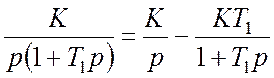 .
.
Тоді маємо
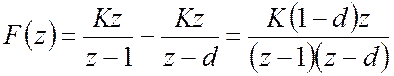 ,
,
де ![]() ,
а
,
а ![]() – період дискретності.
– період дискретності.
Приклад 3. Знайти ![]() -перетрорення
для функції часу, котра має таке зображення Лапласу
-перетрорення
для функції часу, котра має таке зображення Лапласу
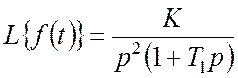 .
.
Початкові дані: ![]() ,
,
![]() , період дискретності
, період дискретності ![]() .
.
Відповідь:
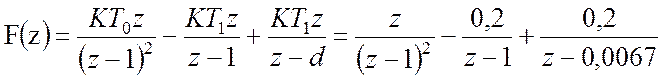 ,
,
де ![]() .
.
Приклад 4. Знайти ![]() -перетрорення
для функції часу
-перетрорення
для функції часу
![]()
у трьох випадках: 1) 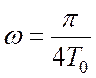 ; 2)
; 2) 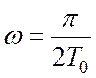 ;
3)
;
3) 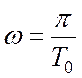 .
.
Відповідь:
1) 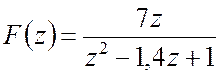 ; 2)
; 2) 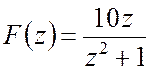 ; 3)
; 3) ![]() .
.
Приклад 5. Дано ![]() -перетрорення
дискретної функції часу
-перетрорення
дискретної функції часу
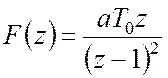 ,
,
де ![]() –
період дискретності. Визначити початкову функцію часу у точках
–
період дискретності. Визначити початкову функцію часу у точках ![]()
![]() .
.
Розв’язання.
Ділення чисельника на знаменник дає нескінченний ряд (ряд Лорану)
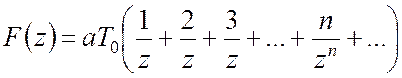 .
.
Звідси можна отримати
![]() .
.
Приклад 6. Дано ![]() -перетрорення
дискретної функції часу
-перетрорення
дискретної функції часу
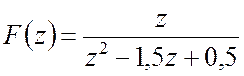 .
.
Знайти початкову гратчасту функцію часу розкладенням на прості дроби.
Розв’язання.
Знайдемо корні рівняння
![]() .
.
Значення коренів: ![]() ,
, ![]() .
Далі подамо
.
Далі подамо ![]() у вигляду простих дробів
у вигляду простих дробів 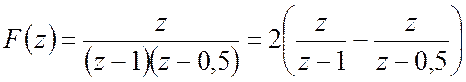 .
.
Перший доданок праворуч відповідає оригіналу ![]() , а другий –
, а другий – ![]() , причому
, причому ![]() . Тому для оригіналу можна записати
. Тому для оригіналу можна записати
![]() .
.
Приклад 7. Знайти ![]() -перетрорення
для функції часу
-перетрорення
для функції часу
![]() ,
,
визначеної при ![]() в
дискретні моменти часу
в
дискретні моменти часу ![]() .
Початкові дані:
.
Початкові дані: ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Відповідь:
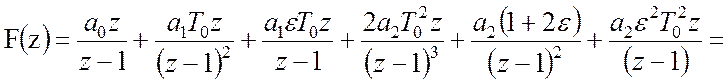
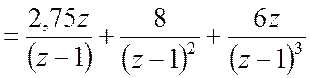 .
.
Приклад 8. Визначити оригінал ![]() по зображенню у
вигляді дрібно-раціональної функції
по зображенню у
вигляді дрібно-раціональної функції
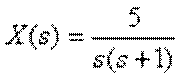 .
.
Розв’язання.
Використаємо розклад Хевісайда для дрібно-раціональної функції з одним нульовим полюсом. Тоді
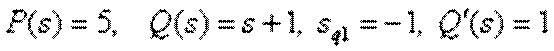 .
.
Коефіцієнти розкладу мають вигляд
![]() .
.
Зображення у формі Хевісайда має вигляд
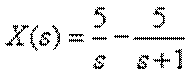 .
.
Використаємо теорему про лінійність а також й таблицю перетворень для кожного доданка, в результаті отримаємо
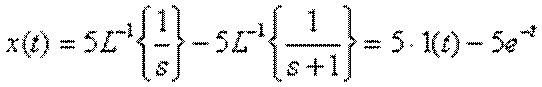 .
.
Графік функції оригіналу має вигляд, показаний на рис. *.
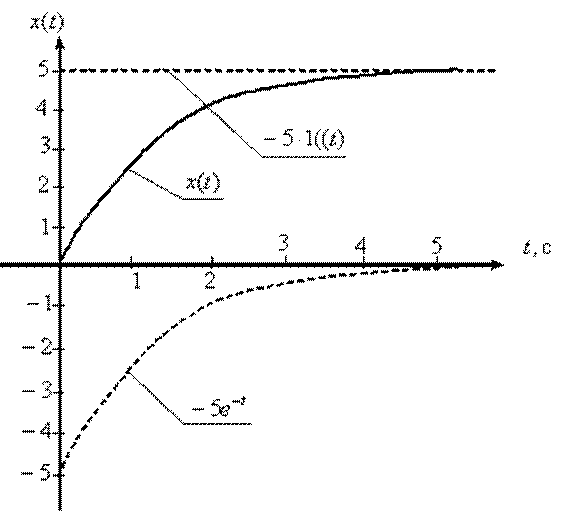
Рис. *
Стисло пояснимо алгоритм розв’язання диференційних рівнянь операторним методом на прикладі розв’язання диференційного рівняння 2-го порядку у загальному вигляді
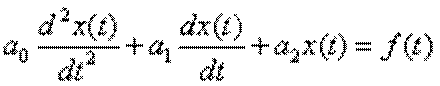 ,
,
де ![]() ,
, ![]() ,
, ![]() .
.
Застосуємо теорему про диференціювання для знаходження зображень похідних
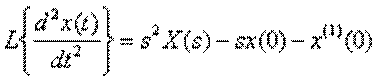 ,
, 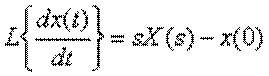 .
.
Нехай ![]() , тоді
, тоді
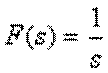 .
.
Отримаємо операторне рівняння, використовуючи теорему лінійності
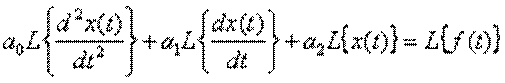 ,
,
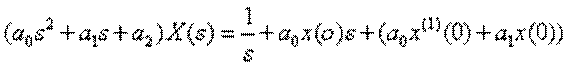 .
.
Розв’язуємо
рівняння відносно ![]() ,
,
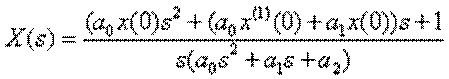 .
.
Знайдемо ![]() , використовуючи розклад Хевісайда
, використовуючи розклад Хевісайда
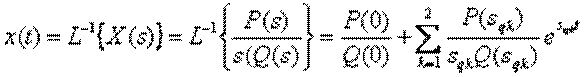 ,
,
де ![]() ,
, ![]() .
.
Особливо
треба пригорнути увагу на отримання зображення східної функції ![]() , котра визначається таким чином:
, котра визначається таким чином:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.