Гратчасті функції. Кінцеві різниці. Обчислення кінцевих різниць, додатків, первісних, страница 2

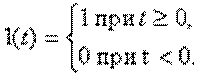
Якщо використовувати

,

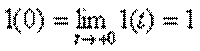то одержимо помилкове розв’язання, тому слід використати так звані „ліві” початкові умови

.

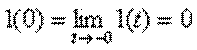Правдивість цього легко перевірити підстановкою рішення до початкового диференційного рівняння.

Приклад 9. Визначте оригінал зображення по Лапласу

.

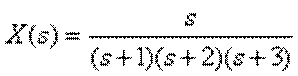Відповідь:

.

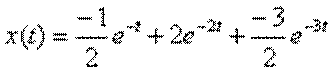Аналіз лінійних розімкнутих імпульсних систем.

Обчислення передатних функцій. Дослідження перехідних

режимів та режимів, що встановилися.

Приклад 1.  Перетворити початкову структурну схему до типового вигляду; визначити неперервну передатну функцію приведеної неперервної частини розімкнутої імпульсної системи , приймаючи за вихідний – сигнал y(t).

Розв’язання.

Початкова структурна система імпульсної САР та вихідний сигнал ІЕ

               

 

                  

                                      

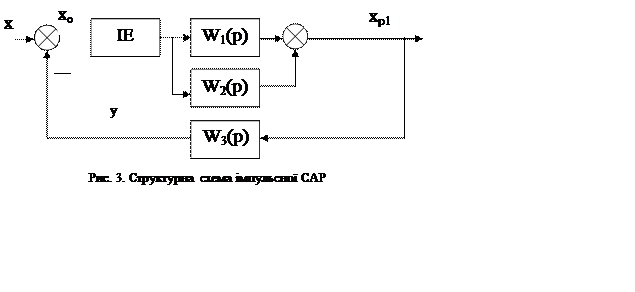
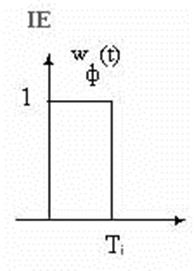
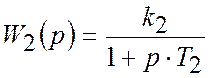
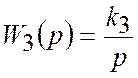
Приведемо до загального вигляду, зображеному на рис. 4.

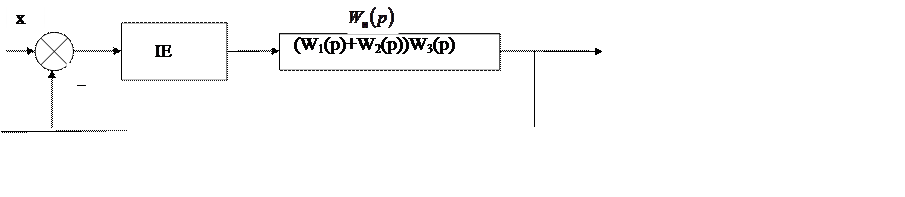
Рис.4. Типова структурна схема імпульсної САР

Запишемо вираз для неперервної передатної функції розімкненої системи:

.

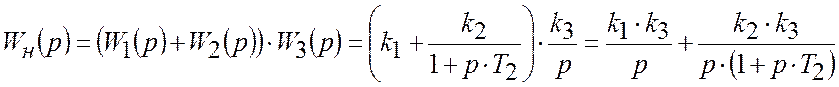Тепер знайдемо передатну функцію розімкненої дискретної системи.

Передаточная функция  формирующего фильтра:

.

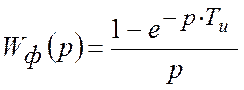T_u – період квантування.

Передатна функція приведеної неперервної частини:

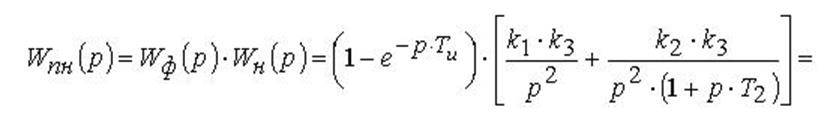
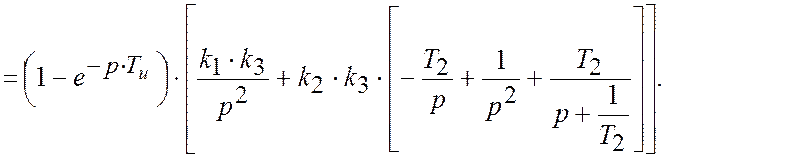
Використовуючи дискретне перетворення Лапласу, отримаємо передатну функцію розімкненої імпульсної системи:

.

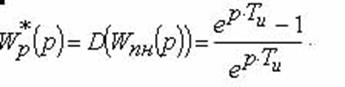
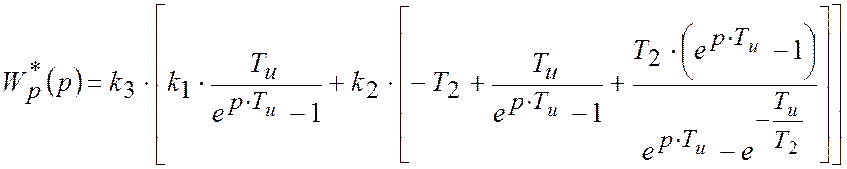В результаті перетворень початкову передатну функцію приводимо до вигляду:

 ,

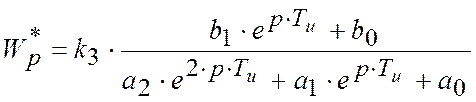де                                 ,          ,

,, ,

,    ;                ,    .

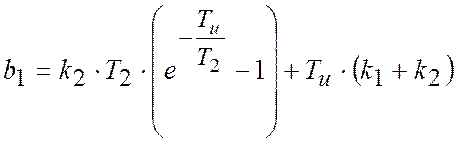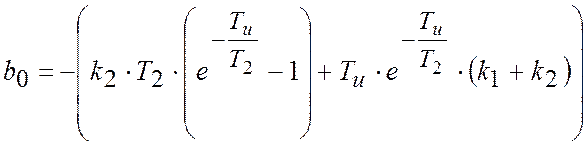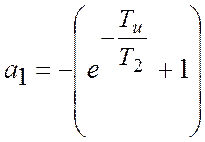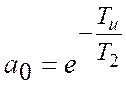Приклад 2.  По  знайти дискретну передатну функцію розімкненої імпульсної системи 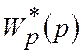 (приклад 1).

Розв’язання.

Передатну функцію цієї імпульсної САР у розімкненому стані можна визначити на основі вагової функції приведеної неперервної частини , згідно наступному співвідношенню:

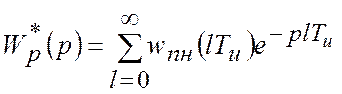
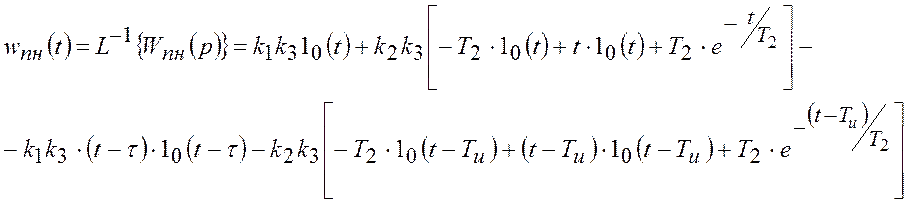
Якщ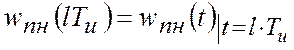о , то:

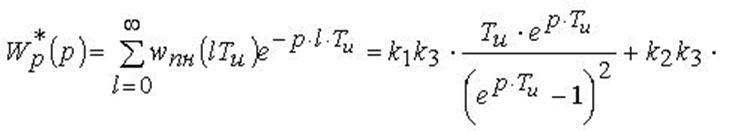
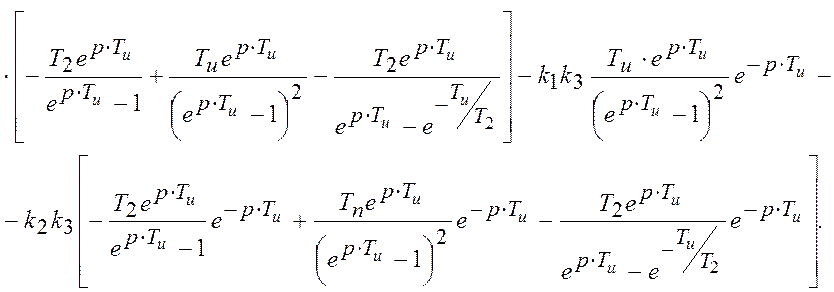
Після перетворень, одержимо шуканий вираз для 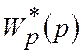, який співпадає з раніше одержаним.

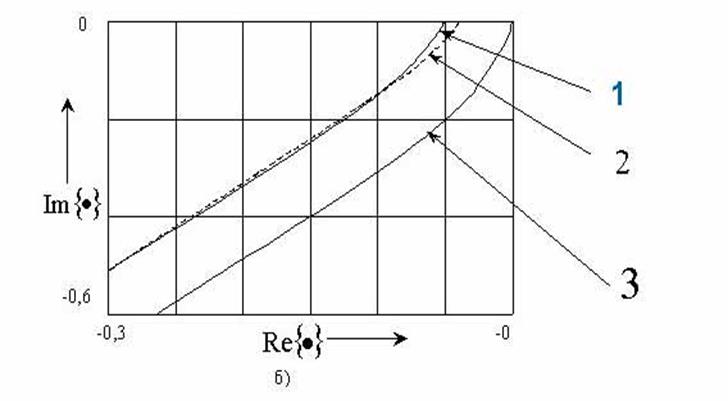
Приклад 3. Побудувати годограф розімкненої імпульсної САР (приклад 1):

a) по виразу ;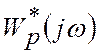

b)   по годографу .

Розв’язання.

Побудуємо годографи імпульсної та неперервної розімкнутої системи.

Годограф імпульсної розімкнутої системи побудуємо двома засобами:

– точним (безпосередньо по знайденої раніше передатній функції);

– приблизним – по формулі:

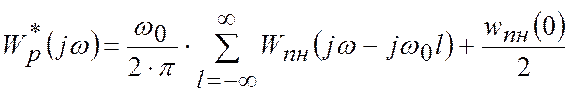
або в приближенні:

,

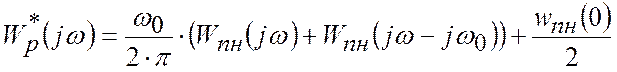де

1

	Рис. 5 Годографи для та

 

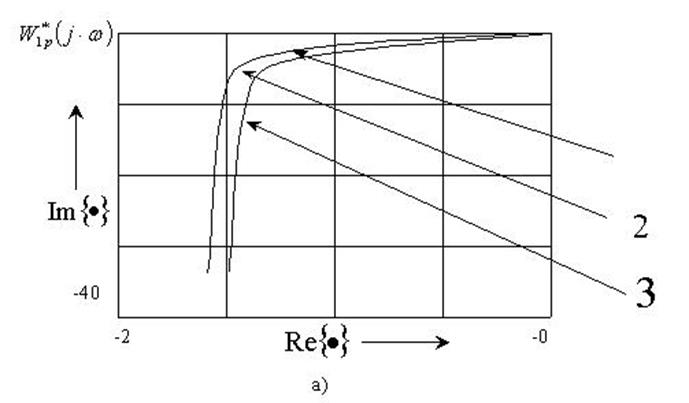
Як видно з рисунку годографи імпульсної розімкненої системи, побудовані точним та приблизним методами співпадають.

Численні значення годографів імпульсної розімкненої системи, побудовані точним та приблизним методами:

	Точный метод	Приблизний метод
n = 1	-0,34-0,579i	-0,34-0,577i
n = 2	-0,133-0,237i	-0,132-0,235i
n = 3	-0,086-0,148i	-0,085-0,145i
n = 4	-0,07-0,106i	-0,068-0,102i
n = 5	-0,062-0,081i	-0,059-0,077i
n = 6	-0,057-0,064i	-0,054-0,059i
n = 7	-0,055-0,052i	-0,05-0,047i
n = 8	-0,053-0,042i	-0,048-0,037i
n = 9	-0,052-0,034i	-0,046-0,029i
n = 10	-0,051-0,027i	-0.044-0,023i
n = 11	-0,051-0,021i	-0,043-0,017i
n = 12	-0,05-0,015i	-0,042-0,012i
n = 13	-0,05-0,01i	-0,041-0,008i
n = 14	-0,05-0,005i	-0,041-0,004i
n = 15	-0,05	-0,041