На основі необхідного та достатнього умов стійкості системи (у плоскості “Z”):
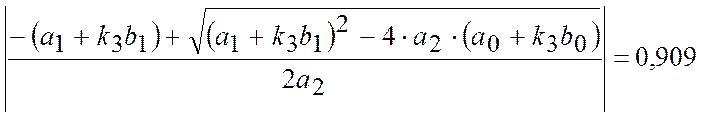
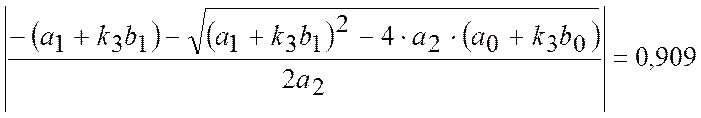 .
.
Корені не виходять з кругу радіусу 1, таким чином система стійка. Граничний коефіцієнт посилення k3 одержуємо з рівняння:
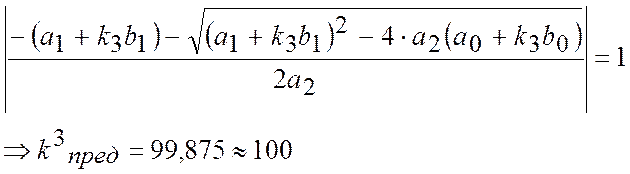
звідси
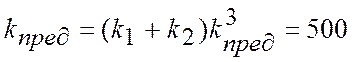
Побудуємо перехідний процес замкненої імпульсної САР.
Для цього перетворимо передатну функцію замкненої імпульсної САР:
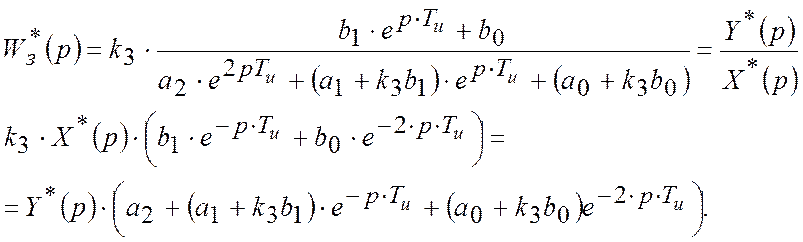
Перейдемо від зображення до оригіналу:
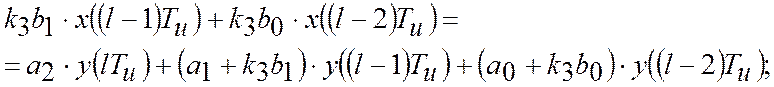
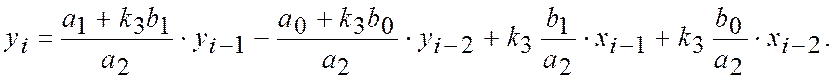
Графік перехідного процесу, побудований на основі останнього співвідношення, зображен на рис. 9.
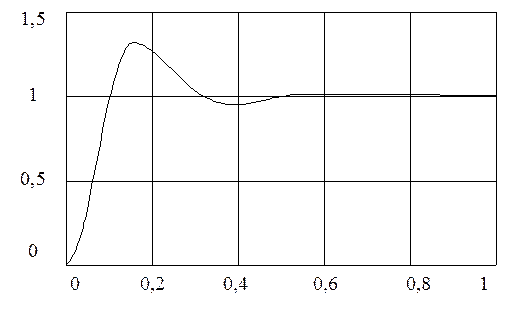

Приклад 2. Визначити статистичну та кінетичну помилки замкненої імпульсної САР.
Розв’язання.
Розрахуємо статистичну та кінетичну помилки замкненої імпульсної САР.
Формули для обчислення помилок:
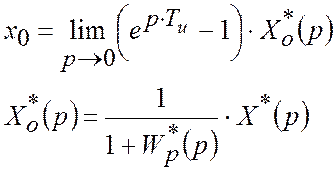
– Статистична
На вході системи X(t) = 1(t)
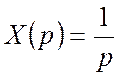
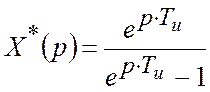
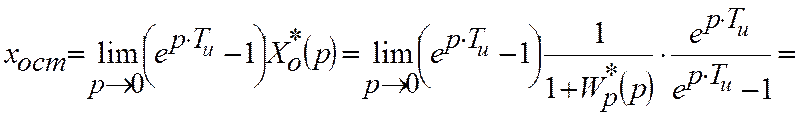
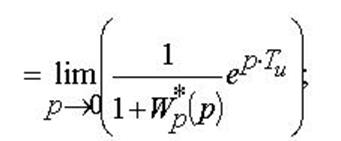
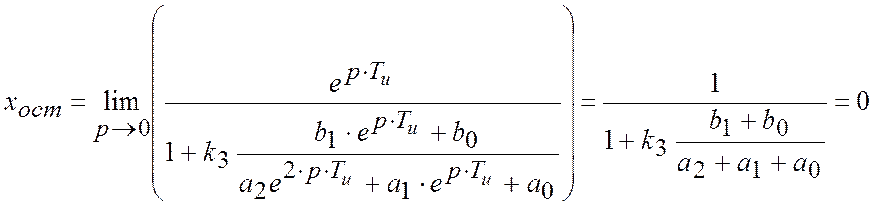
– Кінетична
На вході системи X(t) = t×1(t)
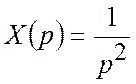
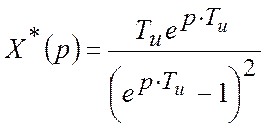
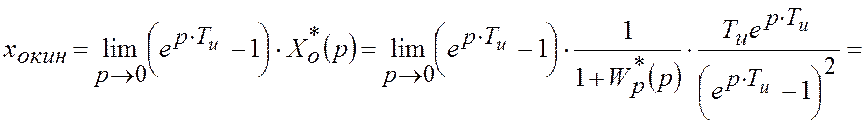
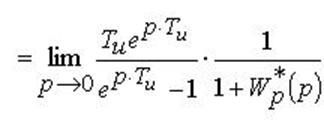
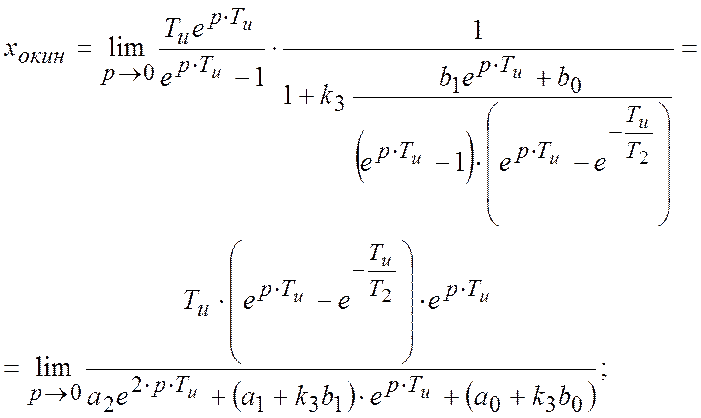
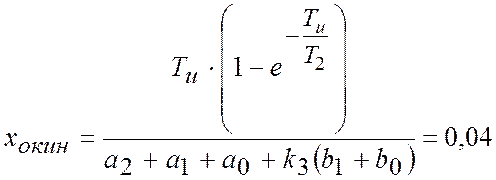 .
.
Приклад 3. Визначити стійкість замкненої імпульсної системи та її граничний коефіцієнт:
а) за критерієм Найквісту;
б) за критерієм Гурвіцу;
в) по кореням характеристичного рівняння.
Побудувати перехідний процес y(t) для замкненої імпульсної САР.
Розв’язання.
– за критерієм Найквісту.
Тому що годограф ![]() не охоплює точку з координатами ( – 1, j0), імпульсна
система у замкненому стані є стійкою.
не охоплює точку з координатами ( – 1, j0), імпульсна
система у замкненому стані є стійкою.
Граничний коефіцієнт визначаємо з співвідношення:
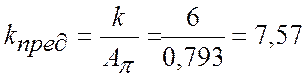
де ![]() –
коефіцієнт посилення замкненої САР;
–
коефіцієнт посилення замкненої САР; ![]() –
модуль комплексного коефіцієнту посилення при його аргументі, який дорівнює –180 градусів.
–
модуль комплексного коефіцієнту посилення при його аргументі, який дорівнює –180 градусів.
– за критерієм Гурвіцу.
Запишемо передатну функцію дискретної САР у
замкненому стані через ![]() -
перетворення:
-
перетворення:
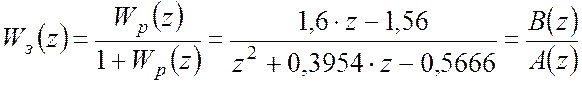 .
.
Введемо підстановку  . Тоді характеристичне рівняння
. Тоді характеристичне рівняння ![]() прийме
вигляд:
прийме
вигляд:
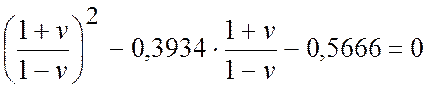
Після перетворення, з останнього співвідношення одержимо:
![]() .
.
Тому що характеристичне рівняння 2-го порядку має всі додатні коефіцієнти, то ця система є стійкою у замкненому стані.
Визначимо ![]() . Для
цього передатну функцію розімкненої імпульсної САР представимо таким чином:
. Для
цього передатну функцію розімкненої імпульсної САР представимо таким чином:
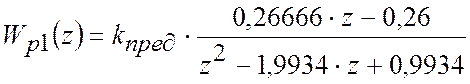 .
.
Зауважимо, що коефіцієнт посилення ![]() дорівнює
дорівнює ![]() .
.
Тоді передатна функція САР у замкненому стані ![]() прийме
вигляд:
прийме
вигляд: 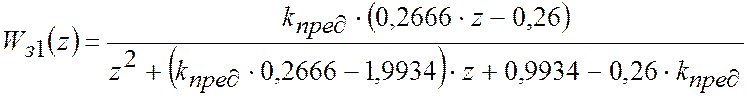 .
.
Підставимо до характеристичного рівняння
відповідно передатній функції ![]() ,
,  . Тоді, після перетворень, одержимо:
. Тоді, після перетворень, одержимо:
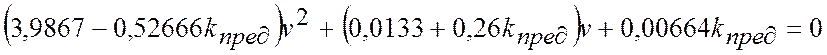 .
.
З умови додатності коефіцієнтів
характеристичного рівняння одержимо ![]() .
.
На основі необхідної та достатньої умов
стійкості. Візьмемо ![]() та
для цього коефіцієнту посилення розімкненої системи визначимо стійкість
замкненої системи на основі коренів характеристичного рівняння.
та
для цього коефіцієнту посилення розімкненої системи визначимо стійкість
замкненої системи на основі коренів характеристичного рівняння.
Для ![]() одержимо:
одержимо:
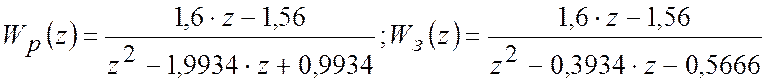 .
.
Звідси корені характеристичного рівняння для замкненої системи дорівнюють:
![]()
тобто 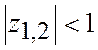 – замкнена
САР є стійкою.
– замкнена
САР є стійкою.
Граничний коефіцієнт посилення знайдемо з рівняння:
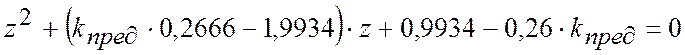 ,
,
звідси
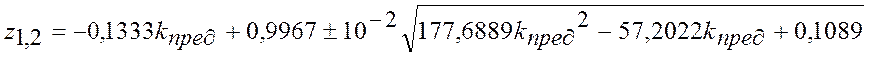 та дорівнявши
та дорівнявши ![]() одержимо значення
одержимо значення ![]() .
.
Побудуємо перехідний процес для замкненої
імпульсної САР при ![]() .
Для цього поділимо чисельник та знаменник
.
Для цього поділимо чисельник та знаменник ![]() на
на ![]() . Тоді
. Тоді
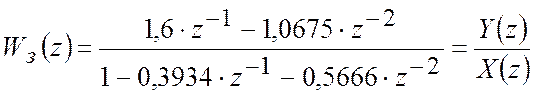 .
.
Перехідний процес можна одержати з наступного
різницевого рівняння, одержаного з виразу для ![]() :
:
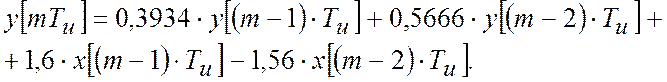
Приклад 4. Визначити статистичну та кінетичну помилки замкненої імпульсної САР.
Розв’язання.
Розрахуємо статистичну та кінетичну помилки замкненої імпульсної САР.
Передатна функція системи відносно помилки:
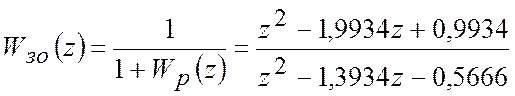 .
.
Тоді статистична помилка при ![]() :
:
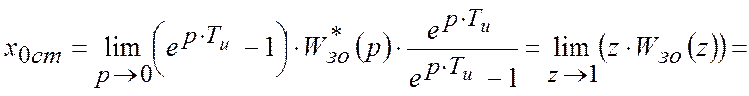
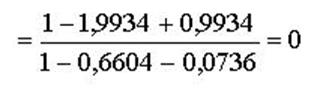
Кінетична помилка має місце, коли вхідною є функція, котра змінюється за лінійним законом:
![]() або
або
![]() .
.
Дискретне перетворення Лапласу вказаного сигналу
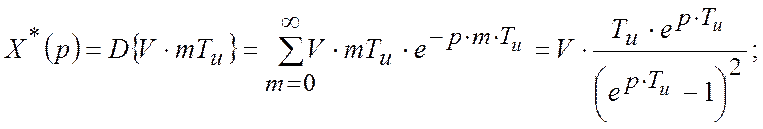
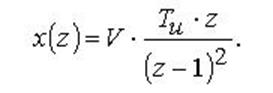
Тоді кінетична помилка дорівнює:
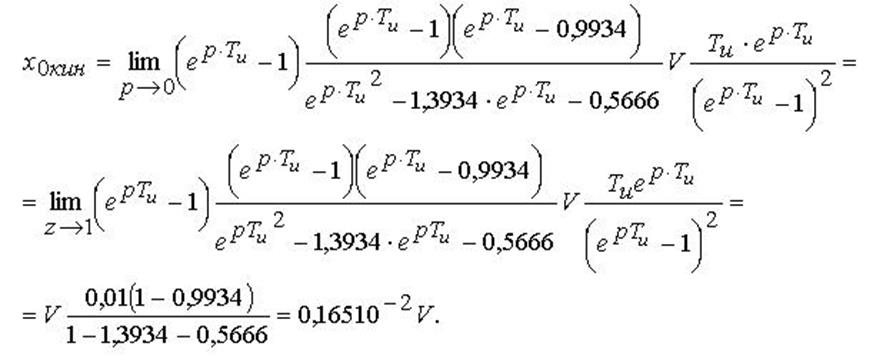
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.