Приклад 4. По
![]() знайти
дискретну передатну функцію розімкненої імпульсної системи
знайти
дискретну передатну функцію розімкненої імпульсної системи 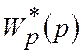 .
.
![]() (час запізнення);
(час запізнення); ![]() ;
;
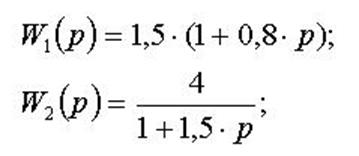
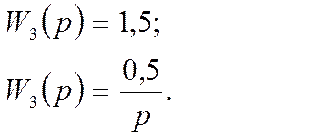
Розв’язування.
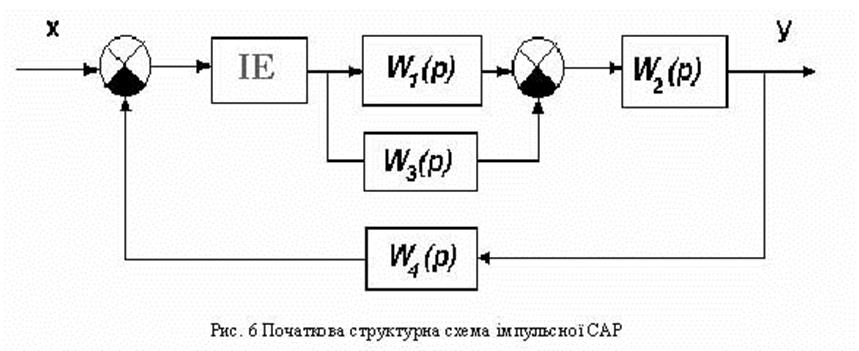
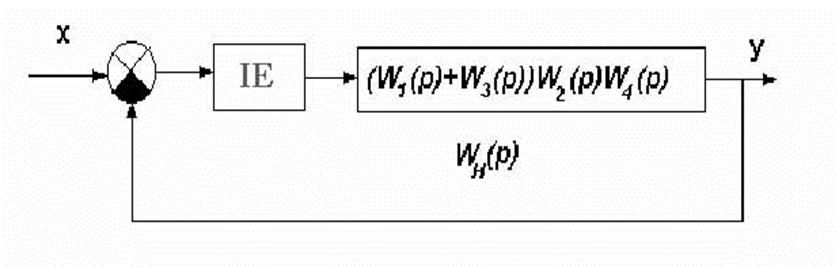
Перетворимо початкову структурну схему до
типового вигляду, зображеному на рис. 7.![]()
![]()
|

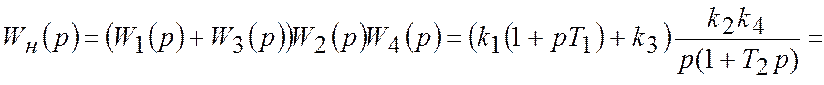 |
![]()
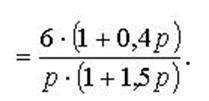
Якщо ![]() , то
, то ![]() .
.
Визначимо вагому функцію для приведеної неперервної
частини САР ![]() .
Для цього представимо
.
Для цього представимо ![]() у вигляді додатку доданок:
у вигляді додатку доданок:
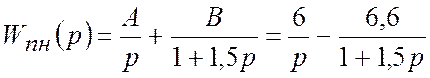 .
.
Тоді
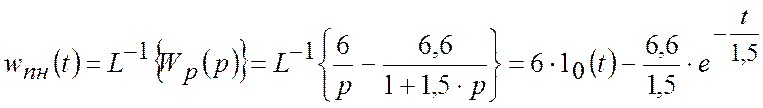 .
.
Згідно умові завдання в імпульсній системі
існує невеличке запізнення (![]() , але не дорівнює нулю), тому в виразі для
дискретного перетворення Лапласу додавання починається не з нульової дискети (
, але не дорівнює нулю), тому в виразі для
дискретного перетворення Лапласу додавання починається не з нульової дискети (![]() ), а з першої дискети (
), а з першої дискети (![]() ). Вважаючи цей факт,
одержимо передатну функцію
розімкненої передатної системи:
). Вважаючи цей факт,
одержимо передатну функцію
розімкненої передатної системи:
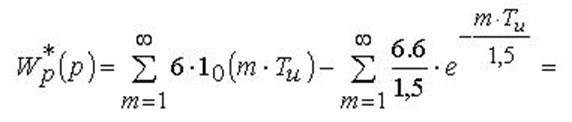
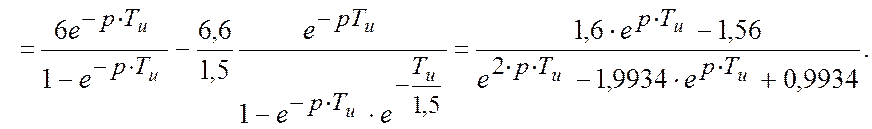
Приклад 5. Побудувати годограф розімкненої імпульсної САР (приклад 4).
Розв’язання.
Побудуємо годограф розімкнутої імпульсної САР, для цього запишемо вираз для комплексного коефіцієнту підсилення:
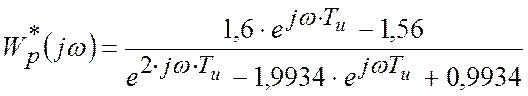 .
.
Використавши формулу Ейлера 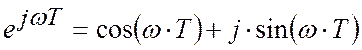 одержимо:
одержимо:
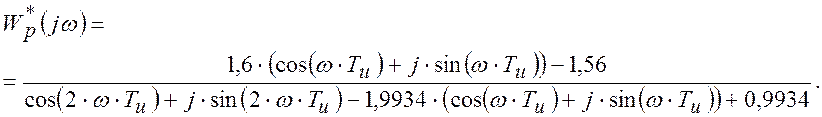
Визначимо у виразі ![]() дійсну (Re) та
уявну (Im) частки, для цього необхідно перетворити знаменник
виразу
дійсну (Re) та
уявну (Im) частки, для цього необхідно перетворити знаменник
виразу ![]() ; помножити чисельник та знаменник на
комплексно-спряжене знаменнику число; та знову здійснити перетворення
; помножити чисельник та знаменник на
комплексно-спряжене знаменнику число; та знову здійснити перетворення
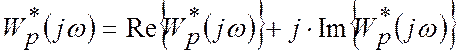 .
.
Значення ![]() та
та
![]() , одержані для різних
, одержані для різних ![]() , записані у таблиці 1, а годограф імпульсної
САР зображен на рис. 8.
, записані у таблиці 1, а годограф імпульсної
САР зображен на рис. 8.
|
|
50 |
100 |
200 |
450 |
700 |
900 |
1200 |
1800 |
|
|
– 4.67 |
– 1.762 |
– 1,032 |
– 0,836 |
– 0,808 |
– 0,8 |
– 0,795 |
– 0,793 |
|
|
– 18,28 |
– 9,012 |
– 4,458 |
– 1,896 |
– 1,121 |
– 0,785 |
– 0,453 |
0 |
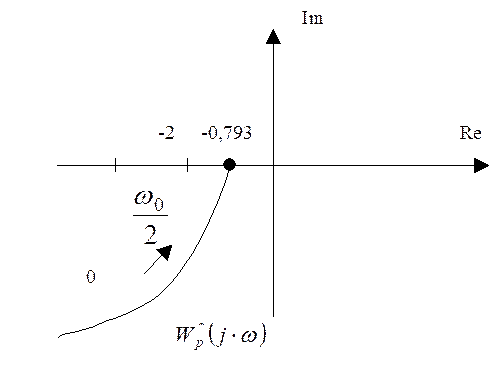

Будування годографа ![]() по
годографу
по
годографу ![]() здійснюється згідно виразу:
здійснюється згідно виразу:
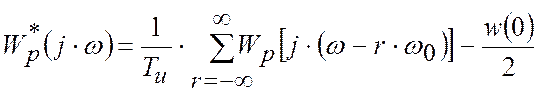 .
.
Тому що ряд для ![]() з
зростанням w збігається
дуже повільно, число членів ряду для будування
з
зростанням w збігається
дуже повільно, число членів ряду для будування ![]() повинно
бути не менш ніж три.
повинно
бути не менш ніж три.
Аналіз лінійних замкнених імпульсних систем.
Обчислення передатних функцій. Дослідження
перехідних процесів та процесів, що встановилися,
стійкості замкнених імпульсних систем.
Приклад 1. Оцінити стійкість замкненої імпульсної САР та знайти граничний коефіцієнт посилення:
а) за критерієм Найквісту;
б) за критерієм Гурвіцу;
в) по кореням характеристичного рівняння.
Побудувати перехідний процес y(t) для замкненої імпульсної САР
Розв’язання.
Визначимо стійкість замкненої імпульсної системи та її граничний коефіцієнт:
– за критерієм Найквисту:
Годограф розімкненої імпульсної системи не охоплює точку ( – 1; j0) – замкнена система стійка.
Значення граничного коефіцієнту посилення розімкненої імпульсної системи знайдемо з пропорції:
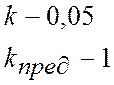 , звідки
, звідки ![]()
– за критерієм Гурвіцу:
Знайдемо передатну функцію замкненої імпульсної САР, за допомогою коефіцієнту посилення k3:
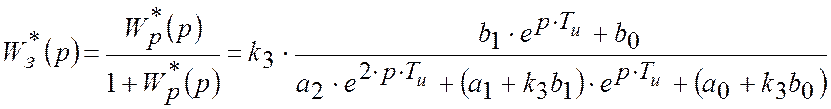 .
.
Введемо позначку ![]() та запишемо характеристичне рівняння:
та запишемо характеристичне рівняння:
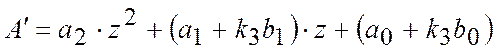 .
.
Зробимо підстановку:

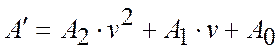 ,
,
де
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Тому що всі коефіцієнти ![]() додатні, замкнена САР стійка.
додатні, замкнена САР стійка.
Найбільш просто з приведених вище формул знайти значення граничного коефіцієнту посилення:
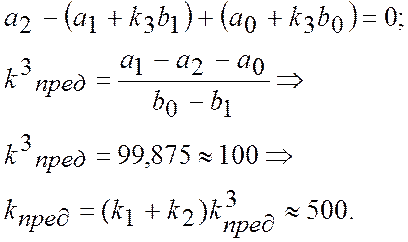
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.