Решение. Задача решается с помощью двух преобразований. Первым (решение исходной задачи 2, изложенной выше), а вторым полученная проецирующая плоскость переводится в положение плоскости уровни. Точки А5, В5 и С5 расположены от оси Х, разделяющей плоскости П4 и П5, на расстояниях, равных величинам координат Y для точек А, В и С в системе плоскостей проекций П1-П4.
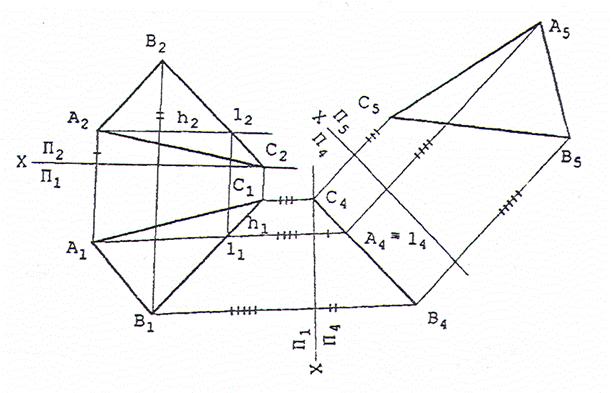
Решение рассмотренной задачи позволяет находить натуральные величины плоских фигур (следовательно, сторон многоугольников и плоских углов).
Задача №4. Построить наклонное сечение пирамиды проецирующей плоскостью (натуральную величину сечения).
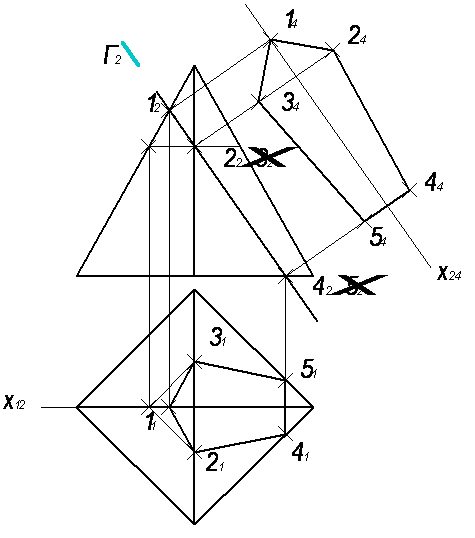
Пирамида – непроецирующая поверхность, плоскость является фронтально-проецирующей. Отсюда следует, что одна проекция линии пересечения имеется и совпадает с фронтально-проецирующей плоскостью. Вторую проекцию линии пересечения строим по принадлежности к первой. Соединив проекции точек 1, 2, 3, 4, 5, на П1 получим горизонтальную проекцию линии пересечения.
Для определения натуральной величины сечения введем новую плоскость П4 параллельно фронтально-проецирующей плоскости.
Ось Х1, 2 проведем через проекцию точки 11; ось Х2, 4 – параллельно секущей плоскости на фронтальной плоскости проекций. Проведем линии связи перпендикулярно оси Х2, 4 и перенесем проекцию линии пересечения с П1 на П4. Соединив проекции этих точек на П4, получим натуральную величину сечения.
Построить натуральную величину сечения конуса фронтально проецирующей плоскостью.

Тема 6. «Развертывание поверхностей. Особенности построения разверток различных поверхностей».
Модуль - развертывание поверхностей.
Ключевые слова: поверхность, развертка, плоская фигура, способ нормальных сечений, способ раскатки, способ треугольников.
Начинать самостоятельную работу по данному разделю рекомендуется с изучения классификации поверхностей по признаку развертываемости. Необходимо уяснить способы построения разверток развертываемых поверхностей и условных разверток неразвертываемых поверхностей.
Вопросы для изучения теоретической части темы
1).Какие поверхности называются развертываемыми?
2).Какая плоская фигура получается при развертке боковой поверхности прямого круглого цилиндра?
3). Какие линии получаются при пересечении гранных поверхностей?
Тесты
1. Что называется разверткой поверхности
а) плоская фигура, которая получается путем совмещения всех точек поверхности с плоскостью без складок и разрывов
б) плоская фигура, которая получается путем совмещения части точек с другой поверхностью
в) плоская фигура, которая получается с поверхность путем плоско-параллельного перемещения.
2. Какие поверхности относятся к не развертывающимся
а)конус
б)сфера
в) цилиндр
3. Какую форму имеет развертка прямого кругового конуса
а)прямоугольник
б)треугольник
в)сегмент круга
4. Какую форму имеет развертка прямого кругового цилиндра
а)прямоугольник
б)треугольник
в)сегмент круга
5. Какими способами можно построить развертку пирамиды
а)способом раскатки
б)способом прямоугольников
в)способом треугольником
Задачи для отработки практической части темы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.