Промежуточные точки 1 гипербол строятся при помощи параллели с. Через произвольно выбранную точку 13 (профильная проекция точки 1) проводится профильная проекция параллели, положение которой на видах спереди и сверху определяется с помощью точки, расположенной на главном фронтальном меридиане. Фронтальные и горизонтальные проекции точек 1 находятся на пересечении линий связи с проекциями параллели на соответствующих видах. Завершается построение соединением полученных проекций точек в гиперболы при помощи лекала.
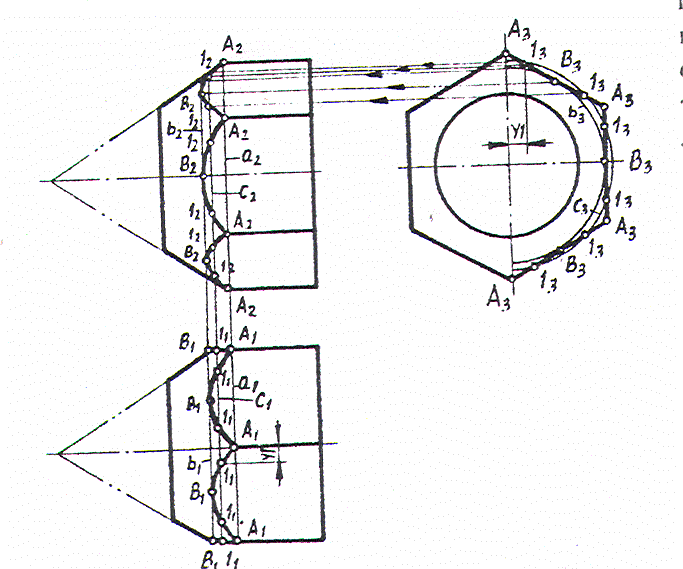
Задача №5.
Построить фронтальную проекцию линии пересечения цилиндра и конуса.
При этом оси поверхностей пересекаются в точке О и параллельны фронтальной плоскости проекций.
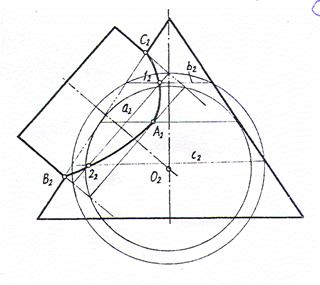
Проведем сферу с центром О так, чтобы она пересекала и цилиндр, и конус. Проведенная сфера будет пересекать поверхность цилиндра по окружности а, которая проецируется в отрезок прямой, соединяющий точки пересечения очерковых линий сферы и цилиндра. Сфера будет пересекать поверхность конуса по двум окружностям b иc, которые спроецируются в отрезки прямых, соединяющих точки пересечения очерковых линий сферы и конуса. Окружность а пересечет окружность b в точке 1, окружность с в точке 2, которые принадлежат линии пересечения цилиндра и конуса.
Для построения проекций точек линии перехода годится не любая сфера. Самая минимальная сфера должна касаться одной из поверхностей и пересекать вторую. С помощью такой сфера построена проекция характерной точки А.
Так как оси цилиндра и конуса параллельны фронтальной плоскости проекций, то точки пересечения проекций главных фронтальных меридианов (В2 и С2) также принадлежат проекции линии пересечения.
Типовое контрольное задание
Задание № 1
Построить проекции линии пересечения призмы и трехгранной пирамиды.

Задание № 2
Построить проекции линии пересечения сферы и призмы.

Задание №3.
Построить проекции линии пересечения двух поверхностей.
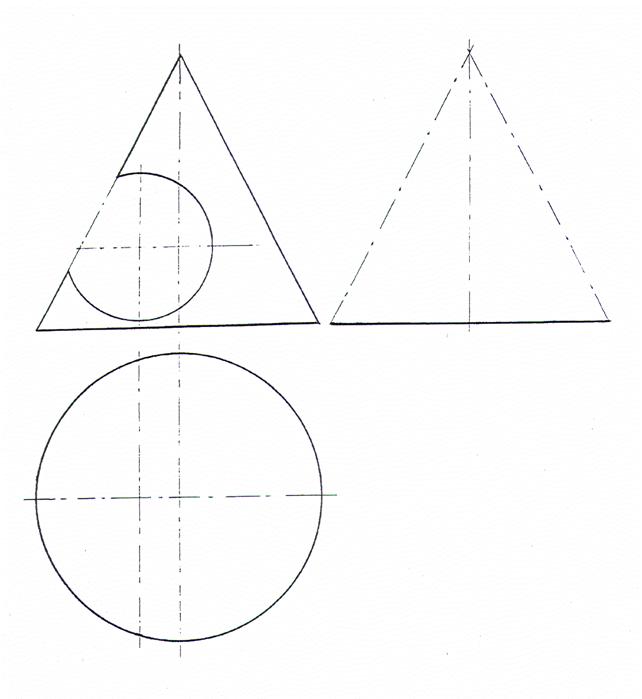
Задание №4.
Построить проекции линии пересечения двух поверхностей.

Тема 5. «Метрические задачи. Способы определения натуральной величины отрезка прямой и плоской фигуры. Наклонные сечения.»
Модуль – метрические задачи.
Ключевые слова: чертеж, преобразование, натуральная величина, отрезок.
Самостоятельная работа по данному разделу дисциплины начинается с изучения способов преобразования чертежа. Особое внимание следует уделить способу замены плоскостей проекций.
Вопросы для изучения теоретической части темы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.