Методические рекомендации по организации самостоятельной работы для студентов специальностей 1706, 0702, 2701, 2703, 2704, 2705, 2707, 2708, 2710, 2712, 2713, 3511 очной и заочной форм обучения, страница 9

1). Сколько преобразований необходимо для определения натуральной величины плоской фигуры?

2). Как располагается новая ось относительно проекций отрезка прямой при определении натуральной величины отрезка?

3). Как располагается плоскость проекций относительно прямой при определении натуральной величины отрезка?

Тесты

1.В каком случае прямой угол проецируется без искажения

а) во всех случаях проецирования

     б) если одна из его сторон параллельна плоскости проекций, а другая ей не перпендикулярна

     в) если одна из ее сторон перпендикулярна плоскости

2. Сколько преобразований необходимо выполнить для определения натуральной величины отрезка (методом замены плоскостей проекции).

а) одна

     б) две

     в)три

3.  В какое положение необходимо преобразовать две пересекающиеся плоскости, чтобы определить угол между ними

а) в проецирующее

     б) в общее положение

     в) в параллельное плоскостям

4.  Сколько преобразований необходимо выполнить для преобразования прямой общего положения в проецирующую прямую (методом замены плоскостей проекции).

а) одна

     б) две

     в) три

5.  Как нужно расположить новую плоскость проекций, чтобы плоскость общего положения стала проецирующей

а) параллельно

     б) перпендикулярно

     в) под углом 45⁰

6.  Какая фигура получается при пересечении призмы плоскостью

а) окружность

     б) эллипс

в)многогранник

7.  Какая фигура получается при пересечении прямого кругового конуса (ось конуса  перпендикулярен p₁) плоскостью горизонтального уровнения

а) эллипс

     б) круг

     в)парабола

Задачи для отработки практической части темы

Задача №1. Преобразовать прямую общего положения (АВ) в прямую уровня. Для решения задачи введем новую фронтальную плоскость проекций П₄, расположенную параллельно горизонтальной проекции А₁В₁ прямой (АВ). Т.к. при проведении новой фронтальной плоскости проекций координаты Z точек А и В не изменяются, дальнейшие построения ясны из чертежа, причем проекция А₄В₄ представляет собой натуральную величину отрезка [АВ]. Таким образом, решение рассмотренной задачи преобразования комплексного чертежа представляет собой еще один способ нахождения натуральной величины отрезка прямой общего положения.

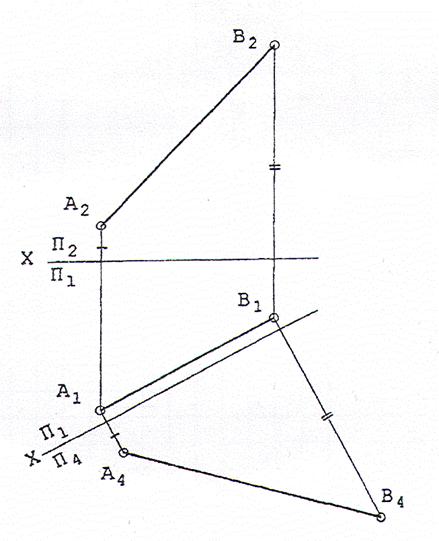
Задача №2. Перевести плоскость общего положения, заданную треугольником АВС, в проецирующую.

Решение. Плоскость, заданная любым способом, представима как множество соответствующих прямых уровня – либо ее горизонталей, либо фронталей. Поэтому преобразования нужно проводить так, чтобы прямых уровня плоскости спроецировались в точки. Тогда плоскость спроецируется в совокупность точек, расположенных на одной прямой. Следовательно, если в заданной плоскости общего положения провести прямые какого-либо уровня, то, расположив новую плоскость проекций перпендикулярно горизонтальной проекции горизонтали или фронтальной проекции фронтали плоскости, можно получить соответствующую проецирующую плоскость.

Такой подход позволяет находить расстояния от точки до прямой, между плоскостью и параллельной ей прямой, между параллельными плоскостями.

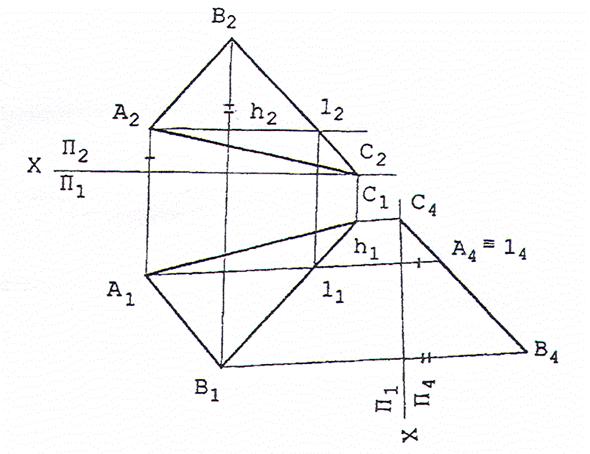
Задача №3. Плоскость общего положения, заданную треугольником АВС преобразовать в плоскость уровня.