Методические рекомендации по организации самостоятельной работы для студентов специальностей 1706, 0702, 2701, 2703, 2704, 2705, 2707, 2708, 2710, 2712, 2713, 3511 очной и заочной форм обучения, страница 6

Типовое контрольное задание

Найти недостающие проекции точек на поверхностях.

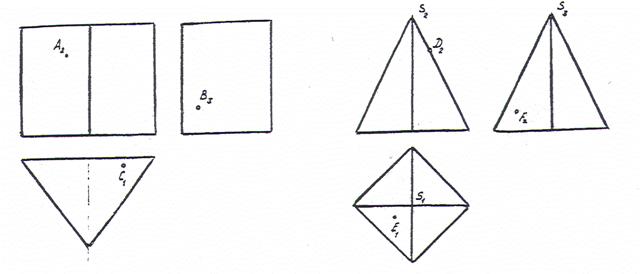
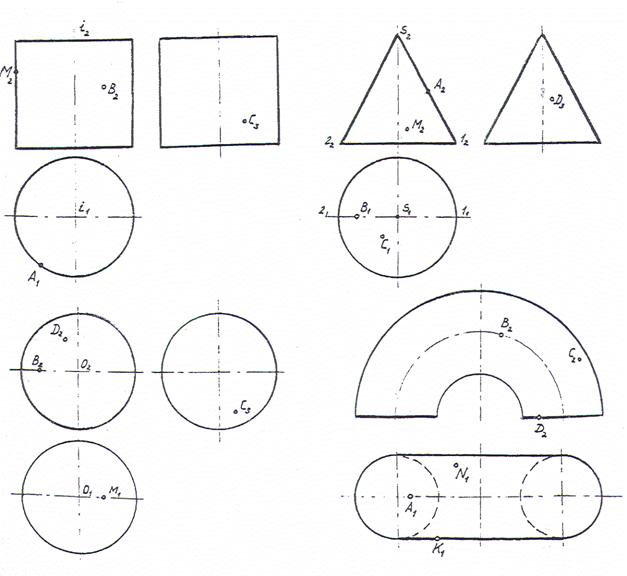
Тема 4 «Графопозиционные задачи. Правила построения линии пересечения двух поверхностей».

Модуль – графопозиционные задачи.

Ключевые слова: линия пересечения, плоскость-посредник, сфера-посредник, проецирующая поверхность.

Самостоятельная работа по данному разделу начинается с изучения способов построения точки пересечения прямой и плоскости и построения линии пересечении плоскостей и поверхностей.

Вопросы для изучения теоретической части темы

1)  Алгоритм построения линии пересечения прямой и плоскости.

2)  К чему сводится задача на построение линии пересечения гранного геометрического тела с телом вращения.

3)  Какая фигура получается при пересечении призмы плоскостью.

4)  В каких случаях применяются в качестве посредников плоскости?

5)  Когда применяются сферы посредников?

Тесты

1.  Как строят линию пересечения двугранных геометрических тел.

а) задача сводится к методу плоскостей посредников;

     б) задачи сводится к построению линии пересечения двух плоскостей и построению точки пересечения прямой и плоскости;

     в) задача сводится к методу сфер-посредников.

2.  К чему сводится задача на построение линии пересечения гранного геометрического тела с телом вращения.

а) к построению линии пересечения: плоскости с поверхностью вращения и к построению точки пересечений прямой с поверхность вращения.

     б) к методу плоскостей посредников.

     в) к методу сфер-посредников.

3.  В каких случаях применяются в качестве посредников сферы.

а) во всех случая построения и пересечения поверхностей.

     б) при проецирующих поверхностях.

     в) при не проецирующих поверхностях тел вращения, если оси их пересекаются.

Задачи для отработки практической части

Задача №1.Построить проекцию линии пересечения двух плоскостей общего положения. Для решения этой задачи рассмотрим две плоскости, заданные проекциями треугольников АВС и КЕД.

В плоскости КЕД заключим прямую КД в проецирующую плоскость-посредник . Тогда плоскость пересекает СВ в т.1, а СА – в точке 2. Найдем проекции т.1 и 2 на горизонтальной плоскости проекций. Соединив 1₁ и 2₁ , находим F₁ – точку пересечения прямой 1, 2 с КД на горизонтальной плоскости проекций. Спроецируем F на П₂.

Аналогичным образом определим т.G, заключив АВ в проецирующую плоскость Г. Соединив т. F и G, получим проекцию линии пересечения.

Видимость сторон треугольника определяем методом конкурирующих точек отдельно для горизонтальной и фронтальной плоскостей проекций.

Даны плоскости:(А, В, С); Т (D, Е, К).

Построить линию пересечения плоскостей MN =  Т.