Построение сечения поверхности плоскостью методом перемены плоскостей

Вопрос №8

Построение сечения поверхности плоскостью методом перемены плоскостей. Пояснить на примере.

Рассматривается пример построения сечения конуса плоскостью общего положения Р (рис. 74).

Производится перемена плоскости V:

На следе P_H выбирается произвольно расположенная точка q  и через нее проводится новая ось Х₁ перпендикулярно следу P_H. Строится след P_V1 способом, описанным в предыдущем примере.

Определяется новая проекция вершины конуса – точка s¢₁ (см. рис. 74) и строится новая фронтальная проекция конуса.

Из рис 74 видно, что в системе H, V₁ плоскость Р преобразуется в фронтально - проектирующую плоскость. Эта плоскость пересекает образующие конуса в точках c¢₁ d¢₁. Линия c¢₁ d¢₁ является большой осью эллипса. Разделив отрезок c¢₁ d¢₁ пополам, получают центр эллипса – точку о¢₁.

Строятся горизонтальная и фронтальная проекции большой оси эллипса: через вершину S проводится фронтально – проектирующая плоскость Q и определяется линия пересечения плоскостей Р и Q – TH. На след Q_H проецируются точки о¢₁, c¢₁, d¢₁ – точки о, с, d.

Определяются проекции малой оси эллипса: через точку о¢₁ проводится линия 1 – 2, параллельная оси Х₁. Из точки S производятся засечки радиусом R = 1-2 на линии о - о¢₁ – точки с, f.

Через точку о¢ проводится линия, параллельная оси Х. На эту линию проецируются точки с, f – точки с¢, f¢.

Таким образом, в результате выполненных построений получены проекции большой и малой оси эллипса.

Строятся дополнительные точки сечения конуса плоскостью: на новой фронтальной проекции проводится линия, параллельная оси Х₁ на произвольном размере – линия 3 – 4. Эта линия пересекает след P_V1 в точке к¢₁(l¢₁). Через точку к¢₁ проводится линия, параллельная следу Р_Н. На этой линии производятся засечки радиусом R = 3 – 4 из центра S – точки l, k.

На фронтальной проекции проводится линия, параллельная оси Х на размере, равном расстоянию от точки к¢₁ до оси Х₁. . а эту линию проецируются точки k, l – точки к¢, l¢.

Аналогично строятся проекции точек M, N  сечения и др.

На фронтальной проекции сечение конуса плоскостью представляет видимую и невидимую (пунктирную) линии. С целью определения граничных точек через вершину S конуса проводится горизонтально – проектирующая плоскость S и определяется линия пересечения плоскостей P и S – фронталь, проведенная через точку u¢. Эта линия пересекает сечение в точках a¢ и b¢, являющихся граничными точками видимой линии сечения.

Строится натуральная величина сечения конуса плоскостью:

В системе координат Oxy на оси Ох откладывается большая ось эллипса с центром в точке О, на оси Оу – малая ось эллипса – линии CD и EF.

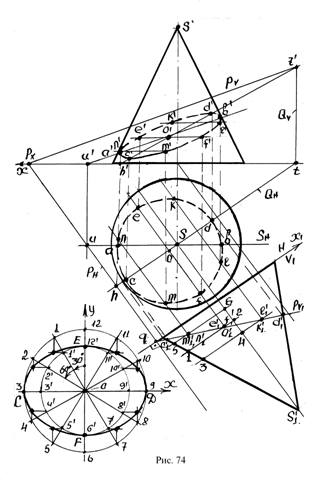
Проводится окружность с центром в точке О и радиусом R = OC и окружность радиусом r = OE.

Через начало системы О проводятся лучи под углом 30° - линии 0 –1, 0 – 2 и т. д. Эти лучи пересекают окружность с радиусом R в точках 1, 2, … 12 и окружность с радиусом r в точках 1¢, 2¢, … 12¢. Через точки 1, 2, … 12 проводятся линии, параллельные Oy, через точки 1¢, 2¢, … 12¢ - параллельные Ох. Пересечение этих линий определяют точки эллипса.