Построение сечения поверхности плоскостью методом граней

Вопрос №6

Построение сечения поверхности плоскостью методом граней

Вопрос №33

Построение развертки многогранника методом  нормального сечения. Пояснить на примере.

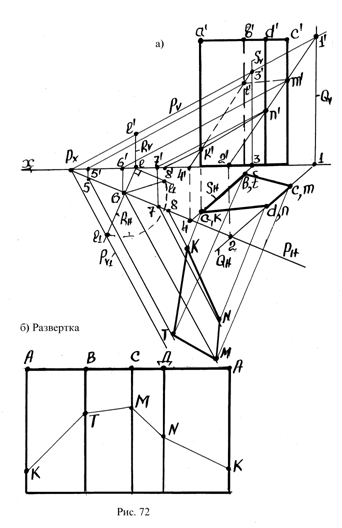
Рассматривается пример построения линии пересечения четырехгранной призмы плоскостью, заданной следами (рис. 72 а):

Через грань cd проводится горизонтально – проектирующая плоскость Q и находится линия пересечения плоскостей P и Q – линия 1 –2 (см. рис. 72 а). На фронтальной проекции определяются точки пересечения ребер d^’ и с¢ с линией 1¢ - 2¢ - точки m¢ и n¢.

Через грань ab проводится проектирующая плоскость S и определяется линия пересечения плоскостей S и Р – линия 3 – 4.

На фронтальной проекции находятся точки пересечения ребер a¢ и b¢ с линией 3^’ – 4^’ – точки k¢ и t¢.

Поскольку ребра пирамиды перпендикулярны плоскости Н, горизонтальные проекции точек KMNT совпадают с точками a, b, c, d.

Соединив на фронтальной проекции точки k¢ n¢ m¢ t¢ линиями, получают проекцию сечения призмы плоскостью.

Для определения натуральной величины сечения используется способ совмещения плоскости Р с плоскостью проекции Н:

На следе Р_V выбирается произвольная точка l¢, через горизонтальную проекцию l проводится линия, перпендикулярная следу Р_Н. От точки пересечения этой линии со следом Р_Н откладывается размер l¢ l – точка l₁. Через точки Р_Х  и l₁ проводится след Р_V1.

Через точки k¢ n¢ m¢ t¢ проводятся линии, параллельные следу P_V (линии t¢ - 5¢, m¢- 6¢, n¢ - 7¢, k¢ - 8¢, см. рис. 72 а).

Определяются горизонтальные проекции точек 5, 6, 7, 8. Через полученные точки проводятся линии, параллельные следу Р_V1.

В результате построений получают проекции фронталей, совмещенные с плоскостью Н. На эти линии проецируются соответственно точки k, n, m, t. Фигура KNMT представляет натуральную величину сечения призмы плоскостью.

Для построения развертки призмы используется способ нормального сечения. Из рис. 72 а видно, что основание призмы перпендикулярно ребрам. Следовательно, за нормальное сечение можно принять основание abcd.

Построение развертки призмы сводится к последовательному построению ее граней, совмещенных с плоскостью проекции (рис 72 б).

Грани призмы представляют собой прямоугольники, одна сторона представляет соответствующее ребро, натуральная величина которого берется с фронтальной проекции. Вторая сторона прямоугольника – соответствующая сторона горизонтальной проекции фигуры anmk.

На развертке находятся точки K, M, N, T, составляющие линию пересечения призмы плоскостью. Натуральные величины отрезков AK, BT, CM, DN снимаются с фронтальной проекции.