Определение натуральной величины треугольника вращением вокруг горизонтали. Построение следов плоскостей

Вопрос №4

Определение натуральной величины треугольника вращением вокруг горизонталь.

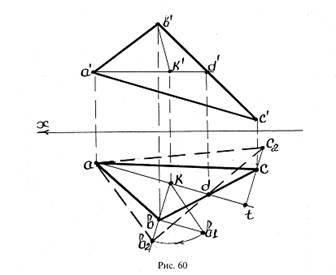
Пример2. Заданы проекции треугольника АВС. Требуется определить натуральную величину фигуры вращением вокруг ее горизонтали (рис.60).

Решение: Проводится горизонталь a’Õ d’  и определяется ее горизонтальная проекция. Прямая АD принимается за ось вращения фигуры.

Определяется центр и радиус вращения точки В. На горизонтальной проекции из точки b опускается перпендикуляр на прямую ad. Точка К – основание  перпендикуляра, является центром вращения точки В.

Находится натуральная величина отрезка BK (отрезок b₁K, см.рис.60).

Определяется центр вращения точки С. Точка t, основание перпендикуляра, опущенного из точки С на прямую ad, является центром вращения точки С вокруг прямой АD.

Прямая ВК поворачивается вокруг оси AD до положения, когда она будет параллельна плоскости Н.

Очевидно, для определения такого положения достаточно прямую b₁k совместить  с прямой  bk  вращением вокруг  точки k (прямая  b₂k , см.рис.60).

При вращении фигуры вокруг оси AD точка С будет перемещаться по прямой, проходящей через точку t и перпендикулярной прямой ad. Следовательно, для  определения нового положения точки С достаточно найти точку пересечения прямых b₂ d и ct – точка С₂.

Точки а, b₂  и  С₂  соединяются прямыми. В результате получают горизонтальную проекцию фигуры а b₂ С₂ , представляющую натуральную величину треугольника АВС.

Вопрос №3, Вопрос №5, Вопрос №7

Построение следов плоскостей

Существует несколько способов построения следов плоскости, заданной на эпюре проекциями трех точек А, В, С.

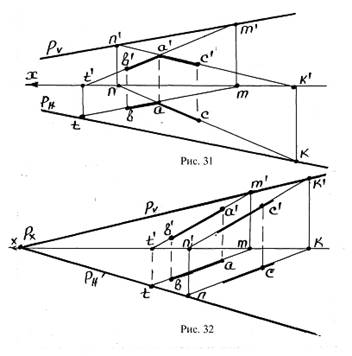
I способ. Через точки А и В проводят прямую АВ и определяют следы прямой на плоскостях V и Н (точки m, t, рис. 31). Затем проводят прямую АС и также находят следы на плоскостях проекций (точки n, k, см. рис. 31).

Через точки m’, n’ проводят след P_V, через точки m, n – след Р_Н.

II способ. Аналогично предыдущему примеру определяются положения точек m, t.

Через точку С проводится линия, параллельная АВ и находятся следы этой линии на плоскостях проекций (точки n, k, рис. 32). Через точки m’, k’ провидится след P_V, через точки  t, n – след Р_Н.

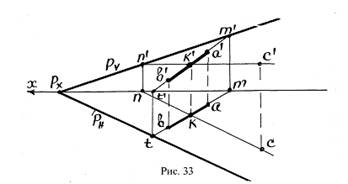
III способ. В отличие от предыдущего примера через точку С проводится горизонталь, имеющая общую точку с прямой АВ (точка k, рис. 33). Определяется горизонтальная проекция точки К и проводится линия ck до пересечения с осью ОХ (точка П). В точке пересечения восстанавливается перпендикуляр и определяется точка П’.

Через точки m’, n’ проводится след P_V, через точку t – след Р_Н, параллельный линии ck.