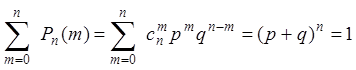 .
.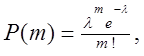 m = 0, 1, 2,
... (2.2)
m = 0, 1, 2,
... (2.2)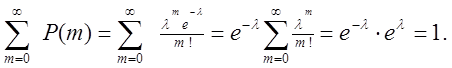
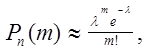
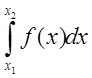 ;
2) f(x) ≥ 0;
;
2) f(x) ≥ 0;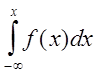 ; 4)
; 4)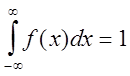 .
.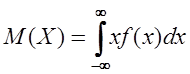 . (2.8)
. (2.8)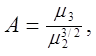 (2.11)
(2.11)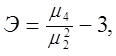 (2.12)
(2.12)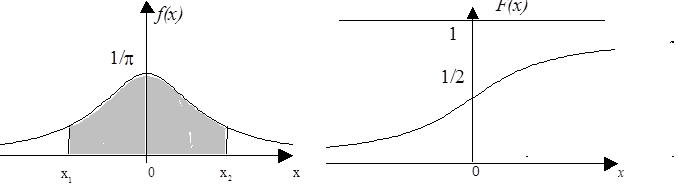
Малюнок 2.1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.