Экономика и менеджмент \ Эконометрика

Економетрика: Навчальний посібник (Статистичні методи аналізу й обробки спостережень), страница 4

Несмещенность, заможність оцінок і їхня лінійність щодо спостережень (для параметрів, що мають размер-ность () - невід'ємна властивість оцінок, використовуваних у мате-матической статистиці. Причина - у математичних зручностях, у значному полегшенні математичного апарата. Несме-щенность інваріантна щодо лінійних преобразова-ний: незалежні незміщені оцінки можна комбінувати й одержувати більш точні незміщені оцінки.

 Побудуємо оцінку для генеральної дисперсії. Візьмемо дисперсію вибірки

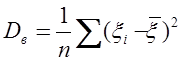
і знайдемо її математичне чекання і дисперсію. Вычисле-ния дають

 ,   .

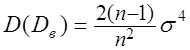Видно, що  є заможної, але зміщеною оцінкою . Однак якщо покласти

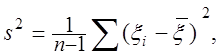                        (2.26)

те, як неважко помітити, вибіркова дисперсія s2 буде незміщеною і заможною оцінкою :

 ,   .                    (2.27)

Очевидно, вибіркова дисперсія s2 менш ефективна, чим Dв, тому що  але вона є незміщеної. У якому клас-сі оцінок дисперсії оцінка s2 буде ефективною? Диспер-сия випадкової величини  має розмірність . Естествен-но зажадати, щоб оцінка дисперсії також мала размер-ность . Найпростіша така функція - квадратична форма від значень вибірки . У силу рівноправності наблюде-ний коефіцієнти при і  повинні бути одинако-вы для всіх і, j (у цьому випадку квадратична форма є сим-метричной).

Визначення5 Оцінка дисперсії є квад-ратичной формою спостережень (квадратична за спостереженнями)  якщо

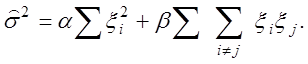                     (2.28)

Теорема 2 Із усіх квадратичних оцінок дисперсії тільки вибіркова дисперсія s2 є незміщеною оцінкою.

Безпосереднє обчислення математичного чекання  (2.28) і наступне виконання умови несмещенности  в даному випадку приводять до результату

 ,  

Підставляючи отримані значення  й  у (2.28), одержуємо

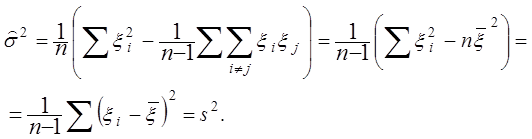
Отже, вибіркова дисперсія s2 є єдиною незміщеною оцінкою генеральної дисперсії в класі квадратичних оцінок. Отже, у даному класі вона є ефективною оцінкою .

Той факт, що для одержання незміщеної оцінки s2 (2.26) у знаменнику вибіркової дисперсії довелося n замінити на   n-1, безпосередньо зв'язаний з тим, що величина  относи-тельно якої беруться відхилення, сама залежить від елементів вибірки. Якби у формулі вибіркової дисперсії були дві такі величини, то n потрібно було б замінити на n-2 і т.д.

Кожна величина, що залежить від елементів вибірки й учас-твующая у формулі вибіркової дисперсії, називається зв'язком. Виявляється, що знаменник вибіркової дисперсії завжди дорівнює різниці між обсягом вибірки n і чис-лом зв'язків , накладених на цю вибірку. Число          r=n- називається числом ступенів волі.

Величина s називається стандартним відхиленням вибірки. Варто сказати, що статистика s не є незміщеною оцінкою для Використання s як оцінку для  занижує значення . Незміщена оцінка  має вид

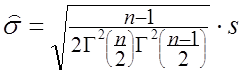 ,                       (2.29)

де Г (х) - гамма-функція. На практиці користаються майже незміщеною оцінкою

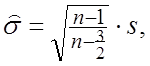                               (2.30)

яка практично збігається з оцінкою (2.29) уже при n ≥ 5.

2.3 Нормальний розподіл і основні вибіркові розподіли, зв'язані з ним

Випадкова величина  називається розподіленої по нормальному законі, якщо її щільність f (х) має вид

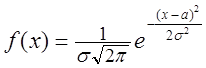 .                        (2.31)

Зміст параметрів а і  наступний :

   .

Середнє квадратическое відхилення  нормальне распреде-ленной величини називається стандартом. У випадку (2.31) пишуть

 ~ N .

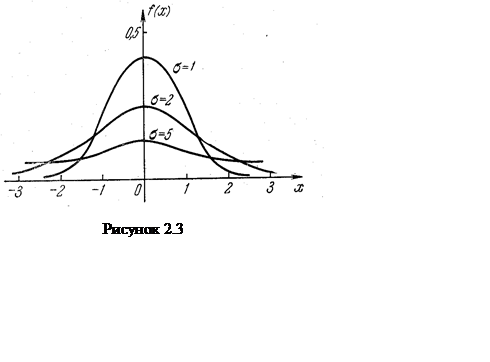
Крива y = f (x) називається нормальної кривої, чи кривої Гаусса. Аналіз кривої Гаусса показує, що вона є сим-метричной відносно прямої х = а й у крапці х = а має максимум. Отже, нормальний розподіл унимо-дальное, і, як і у випадку розподілу Коші (2.15), у нього математичне чекання, медіана і мода збігаються і рівні а.


 При зміні параметра а характер розподілу не міняється, а графік кривої Гаусса лише зміщається чи вправо вліво. Що стосується стандарту , то він істотно впливає на висоту підйому кривої і, отже, на розподіл імовірностей. На мал.2.3 приведені для порівняння три нормальні криві при а = 0 і різних Видно, що зі збільшенням  крутість кривої помітно зменшується. Як наслідок цього - зменшення імовірності улучення випадкової величини в околицю крапки х = а.

Введемо в розгляд величину   Для неї

   ,

тобто

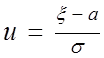 ~ N (0,1).                             (2.32)

Скачать файл