Величина ![]() називається нормованоїі відповідає стандартному нормальному розподілу
називається нормованоїі відповідає стандартному нормальному розподілу
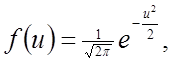
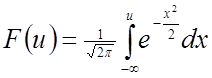 .(2.33)
.(2.33)
Для зручності функцію розподілу можна записати у виді
![]()
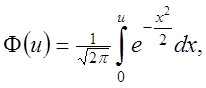 (2.34)
(2.34)
де Ф(u) називається функцією Лапласа. Вона є непарної : ![]() тому таблицю її значень досить скласти
лише для u ≥ 0 (див. додаток
А). У додатку Б приведені також деякі найбільше часто уживані значення величини
u
тому таблицю її значень досить скласти
лише для u ≥ 0 (див. додаток
А). У додатку Б приведені також деякі найбільше часто уживані значення величини
u![]() такий, що Р (
такий, що Р (![]() u
u![]() ) =
) = ![]() при
при ![]()
Зробивши в (2.32) зворотний перехід, одержимо
![]() ~
~ ![]() (2.35)
(2.35)
Якщо ![]() змінюється від х1 до х2,
то
змінюється від х1 до х2,
то ![]() змінюється від
змінюється від ![]() до
до
![]()
![]() Таким чином, для
довільного нормального закону знаходимо
Таким чином, для
довільного нормального закону знаходимо
![]()
![]() (2.36)
(2.36)
Розглянемо абсолютне відхилення ![]() випадкової величини
випадкової величини ![]() (2.35) від свого математичного чекання a.
Думаючи в (2.36)
(2.35) від свого математичного чекання a.
Думаючи в (2.36) ![]()
![]() одержуємо
одержуємо
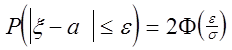
чи, позначаючи ![]()
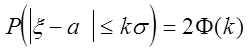 .
.
Зокрема, при ![]() маємо
маємо
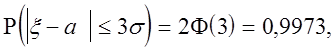
відкіля випливає правило 3![]() : відхилення менші, чим
утроен-ный стандарт, практично достовірні; стосовно до про-тивоположному події це звучить так:
відхилення, великі потроєного стандарту, практично неможливі.
: відхилення менші, чим
утроен-ный стандарт, практично достовірні; стосовно до про-тивоположному події це звучить так:
відхилення, великі потроєного стандарту, практично неможливі.
Нормальний розподіл є найбільш вивченим. Тому його намагаються використовувати і при дослідженні слу-чайных величин, розподілу яких відмінні від нормаль-ного.
Один зі шляхів тут полягає в тім, що розподіл
досліджуваної випадкової величини заміняють приблизно нор-мальным (якщо,
звичайно, це можливо). Так, наприклад, бино-миальное розподіл (2.1) можна
приблизно заміняти нормальним розподілом з параметрами ![]() np,
np,
![]() ; погрішність при цьому буде тим менше, чим більше диспер-сия. У
практичних обчисленнях при р > 0,1 погрішністю переходу можна
зневажати вже при npq ≥
9. Такий підхід особливо
часто використовується при обробці результатів наблю-дений, де звичайно немає
можливості установити розподіл випадкової величини з абсолютною точністю.
; погрішність при цьому буде тим менше, чим більше диспер-сия. У
практичних обчисленнях при р > 0,1 погрішністю переходу можна
зневажати вже при npq ≥
9. Такий підхід особливо
часто використовується при обробці результатів наблю-дений, де звичайно немає
можливості установити розподіл випадкової величини з абсолютною точністю.
Інший підхід у припущенні нормального распреде-ления результатів спостережень складається в побудові статистик, що підкоряються відомим вибірковим розподілам. Це дозволяє будувати довірчі інтервали для неиз-вестных параметрів і перевіряти основні гіпотези матема-тической статистики.
![]() - розподіл (розподіл Пирсона). Нехай
- розподіл (розподіл Пирсона). Нехай ![]() незалежні
стандартні нормальні перемінні
незалежні
стандартні нормальні перемінні ![]() ~N (0,1). Тоді розподіл величини
~N (0,1). Тоді розподіл величини ![]() (“хі-квадрат”):
(“хі-квадрат”):
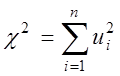
називається ![]() - чи розподілом розподілом
Пирсона з r = n ступенями волі. Воно має щільність
- чи розподілом розподілом
Пирсона з r = n ступенями волі. Воно має щільність
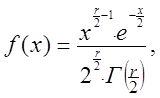 х > 0.
х > 0.
Видно, що ![]() - розподіл не містить невідомих
парів-метрів і залежить тільки від r. Оскільки
- розподіл не містить невідомих
парів-метрів і залежить тільки від r. Оскільки ![]() >
0, те і щільність розглядається лише на проміжку (0,
>
0, те і щільність розглядається лише на проміжку (0, ![]() ).
Графіки плот-ности при деяких значеннях r приведені на мал. 2.4.
).
Графіки плот-ности при деяких значеннях r приведені на мал. 2.4.
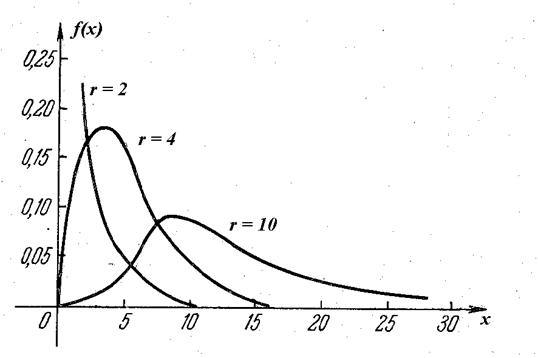 |
Криві асиметричні, і коефіцієнт асиметрії ![]() убуває зі збільшенням r. Це
унимодальное распреде-ление, і його мода m = r-2 зрушується
вправо при збільшенні r. Математичне чекання і дисперсія величини
убуває зі збільшенням r. Це
унимодальное распреде-ление, і його мода m = r-2 зрушується
вправо при збільшенні r. Математичне чекання і дисперсія величини ![]() рівні :
рівні :
![]()
![]()
Виявляється, що деякі статистики вибірки мають ![]() - розподіл. Наприклад, якщо
- розподіл. Наприклад, якщо ![]() -дисперсія нормального розподілу і
-дисперсія нормального розподілу і ![]() - її незміщена оцінка з r = n -
- її незміщена оцінка з r = n -![]() степе-нями волі (
степе-нями волі (![]() - число зв'язків у вираженні для
- число зв'язків у вираженні для ![]() ), те статис-тика
), те статис-тика
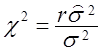 (2.37)
(2.37)
має ![]() - розподіл з r
ступенями волі. Зокрема, якщо значення, що
- розподіл з r
ступенями волі. Зокрема, якщо значення, що ![]() спостерігаються,
( N (a
спостерігаються,
( N (a![]() , ), те незміщеною оцінкою
, ), те незміщеною оцінкою![]() дисперсії є вибіркова дисперсія s2
(2.26), що має r = n - 1 ступенів волі. Тому статистика
дисперсії є вибіркова дисперсія s2
(2.26), що має r = n - 1 ступенів волі. Тому статистика
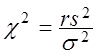 (2.38)
(2.38)
має ![]() - розподіл з числом
ступенів волі r = n - 1.
- розподіл з числом
ступенів волі r = n - 1.
У додатку Г при різних числах
ступенів волі r≤30 приведені
таблиці значень величини ![]() такий, що
такий, що ![]()
![]() (2.39)
(2.39)
при ![]() Для r > 30
перемінна
Для r > 30
перемінна
![]()
приблизно розподілена по стандартному
нормальний зако-ну, тому при r > 30 значення![]() можна
обчислювати по при-ближенной формулі
можна
обчислювати по при-ближенной формулі
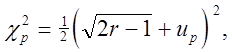 (2.40)
(2.40)
де значення up приведені в додатку Б.
t-розподіл
(розподіл Стьюдента).
Перед-покладемо, що випадкова величина ![]() ~ N (0,1) не залежить від пе-ременной
~ N (0,1) не залежить від пе-ременной![]() , такий, що величина
, такий, що величина ![]() має
має ![]() -
розподіл з r ступенями волі. Тоді розподіл перемінної
-
розподіл з r ступенями волі. Тоді розподіл перемінної
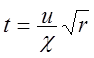 (2.41)
(2.41)
називається чи t-розподілом розподілом Стьюдента з r ступенями волі. Його щільність
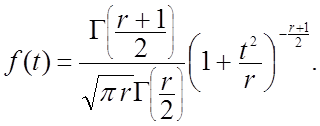
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.