Економетрика: Навчальний посібник (Статистичні методи аналізу й обробки спостережень), страница 3

Визначення 1 Оцінка  щирого значення параметра qназивається незміщеної, якщо по всій сукупності наблю-дений має місце рівність

 .                                           (2.17)

У противному випадку оцінка  для q називається зміщен-ний, причому зсув визначається як .

Визначення 2 Незміщена оцінка  параметра q є ефективної, якщо серед усіх незміщених оцінок для q вона має мінімальну дисперсію.

Визначення 3 Оцінка  параметра q називається заможної, якщо з імовірністю 1   при n  Це означає, що для будь-якого позитивного числа e

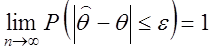 .                         (2.18)

Достатньою умовою заможності оцінки є следу-ющее: при

 ,                              (2.19)

Геометрична інтерпретація вимог, предъявляе-мых до оцінок, що випливає. Оцінку  можна розглядати як центр вибіркового розподілу і вона повинна бути близької до q. Розкид ±δ вибіркового розподілу щодо центра повинний бути якнайменше. При великих обсягах вибірок n вибірковий розподіл повинний мати унимодальную плот-ность розподілу імовірностей (з одним максимумом) і з високим по можливості вузьким піком, крапка максимуму кото-рого (мода) знаходиться біля q (мал. 2.2). Якщо n зростає, пік стає вище і вже, крапка максимуму наближається до q, а міра розкиду δ зменшується. Виходить, повинне бути: при

 ,     δ .                             (2.20)

Порівняння умов заможності оцінки (2.19) і (2.20) показує, що мірою розкиду є дисперсія. Однак у порівнянні з qдисперсія виміряється в квадратних одиницях. Для того щоб мати міру розкиду δ, розмірну з q, вво-дится корінь квадратний з дисперсії, що називають середнім квадратическим відхиленнямвипадкової вес-чини :

(2.21

У приведеній інтерпретації залишився невизначеним центр вибіркового розподілу. На перший погляд, краще інших як оцінку підходить мода вибірки, адже саме в ній щільність унимодального розподілу має максимум. Оцінкою параметра q = а (генерального математичного ожи-дания) можна вибрати також середнє вибірки.

 .                                 (2.22)

Використовуючи (2.16) і властивості математичного чекання і дис-персии (2.14), знаходимо

                  

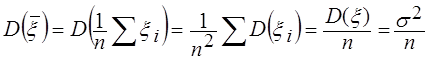           .           (2.23)

Тому що виконуються умови (2.17) і (2.19), те середнє вибірки  є незміщеною і заможною оцінкою генерального математичного чекання. Відзначимо також, що його дисперсія в n раз менше .

Незміщеною і заможною оцінкою генерального математичного чекання є також вибіркова медіана, тому її також можна брати як наближення до щирого результату. У вибіркової медіани є велика перевага перед вибірковим середнім: при досить великому обсязі вибірки її розподіл як випадкової величини близько до нормального (див. ( 2.3) незалежно від того, яке розподіл має генеральна сукупність. Однак у порівнянні з вибірковим середньої вибіркова медіана менш ефективна - її дисперсія в півтора з зайвим разу більше дисперсії середнього. З цієї причини вибіркову медіану рідко використовують при обробці спостережень.

Побудова ефективних оцінок - досить складна зада-ча. Часто найбільш ефективна оцінка досліджуваного параметра взагалі не існує. Тому звичайно мінімізація диспер-сии оцінки здійснюється у визначеному класі оцінок стосовно спостережень (лінійному, квадратичному і т.д.).

Визначення 4 Оцінка параметра qє лінійною комбінацією спостережень (линейна за спостереженнями) якщо

 .                              (2.24)

Коефіцієнти з₁, з₂, ..., сn  називаються вагарнями коэффици-ентами (вагами) розкладання  по

Теорема 1 Із усіх лінійних незміщених оцінок пару-метра а середнє вибірки  має мінімальну дисперсію.

Справді, з (2.24) знаходимо

 ,   .              (2.25)

Тому що  те необхідно покласти

з₀ = 0,   .

Тепер за умови  потрібно мінімізувати . Якщо усі ваги однакові,  тобто з₁ = з₂ = ...= сn =  те . Якщо ж хоча б дві ваги різні, то в силу співвідношення між середнім арифметичним і середньої квадратическим (1.40) . Отже, у класі лінійних не-смещенных оцінок середнє вибірки є ефективною оцінкою оцінюваного параметра a.