На мал. 2.5 приведені
графіки щільності t-розподілу при різних значеннях r. Вони якісно
нагадують за формою щільність стандартного нормального розподілу і наближаються
до нього при ![]() ; випадок
; випадок ![]() відповідає закону N(0,1).
Однак при невеликих r ці криві при збільшенні
відповідає закону N(0,1).
Однак при невеликих r ці криві при збільшенні ![]() значно
повільніше зближаються з віссю абсцис, чим у випадку N(0,1). Тому роль
розподілу Стьюдента особливо велика в статистику малих вибірок. У силу симетрії
відносно прямої t = 0 мода, медіана і математичне чекання збігаються і
дорівнюють нулю, дисперсія
значно
повільніше зближаються з віссю абсцис, чим у випадку N(0,1). Тому роль
розподілу Стьюдента особливо велика в статистику малих вибірок. У силу симетрії
відносно прямої t = 0 мода, медіана і математичне чекання збігаються і
дорівнюють нулю, дисперсія
|
Малюнок 2.5 |
![]() r > 2.
r > 2.
Відзначимо, що при r = 1 розподіл Стьюдента має
вид розподілу Коші (2.15). Таким чином, при ![]() розподіл
Стьюдента приймає всі проміжні положення між розподілом Коші і стандартний
нормальний розподіл.
розподіл
Стьюдента приймає всі проміжні положення між розподілом Коші і стандартний
нормальний розподіл.
Побудуємо конкретні статистики Стьюдента. Нехай неко-торая
оцінка ![]() параметра qлинейна
за спостереженнями, тобто
параметра qлинейна
за спостереженнями, тобто
![]() .
.
У цьому випадку справедливо наступне твердження :
![]() ~
~ ![]() ~
~![]() ,
(2.42)
,
(2.42)
причому згідно (2.25), (2.32)
![]() ,
, ![]() ; (2.43)
; (2.43)
![]() ~ N (0,1). (2.44)
~ N (0,1). (2.44)
Візьмемо в якості![]() -статистики
величину (2.37). Можна показати, що введені в такий спосіб перемінні
-статистики
величину (2.37). Можна показати, що введені в такий спосіб перемінні ![]() і
і ![]() незалежні
і, отже, статистика
незалежні
і, отже, статистика
![]()
![]() (2.45)
(2.45)
має розподіл Стьюдента, причому, як неважко помітити з (2.43), вона не
залежить від генеральної дисперсії ![]() .
.
В окремому випадку, якщо ![]()
![]() = s2, де
= s2, де ![]() і s2 - середнє вибірки і
незміщена вибіркова дисперсія, з (2.23) знаходимо
і s2 - середнє вибірки і
незміщена вибіркова дисперсія, з (2.23) знаходимо ![]() В
результаті статистика (2.45) здобуває вид
В
результаті статистика (2.45) здобуває вид
![]() r = n
- 1. (2.46)
r = n
- 1. (2.46)
Існує багато таблиць розподілу Стьюдента. У додатку В
приведені значення величини ![]() , такий, що при
, такий, що при![]()
![]() .
(2.47)
.
(2.47)
Розглядаються різні варіанти значень a і числа ступенів волі r.
F - розподіл
(розподіл Фишера). Нехай
дві випадкові величини ![]() і
і ![]() мають
мають ![]() -розподіл з r1 і r2
ступенями волі відповідно. Розподіл величини
-розподіл з r1 і r2
ступенями волі відповідно. Розподіл величини
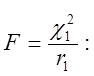
![]() 2.48)
2.48)
називається чи F-розподілом розподілом Фишера з r1 і r2 ступенями волі. З (2.48) випливає, що
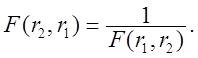 (2.49)
(2.49)
Щільність розподілу Фишера
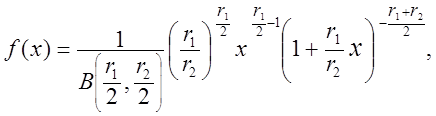
|
Малюнок 2.6 |
де В![]() - бета-функція. При r1
> 2 це унимодальное (одновершинне) розподіл з модою в крапці
- бета-функція. При r1
> 2 це унимодальное (одновершинне) розподіл з модою в крапці ![]() ; його характеристики:
; його характеристики: 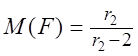 при r2 > 2,
при r2 > 2,
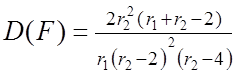 при r2 >
4.
при r2 >
4.
На мал.2.6 приведені графіки f(x)
при сполученнях (r1, r2) = (10,4) і
(10,50). Як і у випадку ![]() -розподілу, плот-ность
розглядається лише на проміжку (0, +
-розподілу, плот-ность
розглядається лише на проміжку (0, +![]() ). Криві мають
асиметричну форму.
). Криві мають
асиметричну форму.
Універсальність F-розподілу підкреслюється
зв'язками з іншими розподілами. При r1=1, r2=r
квадрат величини F(1,r) має розподіл Стьюдента з r
ступенями волі. Якщо r1 = r, ![]() то справедлива тотожність
то справедлива тотожність
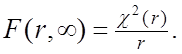 (2.50)
(2.50)
Розподіл Фишера має фундаментальну роль у математичній статистиці і з'явилося, у першу чергу, як розподіл відносини двох вибіркових дисперсій.
Нехай дві випадкові величини ![]() і
і
![]() розподілені нор-мально за законами
розподілені нор-мально за законами ![]() і
і ![]() відповідно,
і нехай
відповідно,
і нехай ![]() і
і ![]() -
незміщені оцінки генеральних дисперсій
-
незміщені оцінки генеральних дисперсій ![]() і
і ![]() зі ступенями волі r1 і r2.
Тоді згідно (2.37) ве-личины
зі ступенями волі r1 і r2.
Тоді згідно (2.37) ве-личины 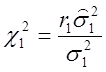 і
і 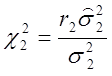 мають
мають ![]() -розподіл
з r1 і r2 ступенями волі відповідно. Тепер
на підставі (2.48) затверджуємо, що перемінна
-розподіл
з r1 і r2 ступенями волі відповідно. Тепер
на підставі (2.48) затверджуємо, що перемінна
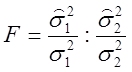 (2.51)
(2.51)
розподілена за законом Фишера з r1 і r2 ступенями волі.
Зокрема, якщо розглядається та сама генеральна
сукупність (а1 = а2, ![]() і отримані дві різні оцінки
і отримані дві різні оцінки ![]() і
і ![]() для
генеральної дисперсії, то з (2.51) одержуємо F-розподіл з r1
і r2 ступенями волі величини
для
генеральної дисперсії, то з (2.51) одержуємо F-розподіл з r1
і r2 ступенями волі величини
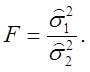 (2.52)
(2.52)
Стосовно до випадку (2.38), коли ![]()
![]() де
де ![]() і
і ![]() дві
вибіркові дисперсії, отримані при різних обсягах вибірок n1 і
n2 відповідно, одержуємо, що відношення двох вибіркових
дисперсій
дві
вибіркові дисперсії, отримані при різних обсягах вибірок n1 і
n2 відповідно, одержуємо, що відношення двох вибіркових
дисперсій
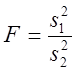 (2.53)
(2.53)
має F-розподіл з n1-1 і n2-1 ступенями волі.
Функція розподілу F(r1, r2) табулирована в багатьох довідкових виданнях. У додатку Д приведені таблиці значень величини Fp(r1, r2), такий, що
P(F(r1, r2) ≤ Fp(r1, r2)) = p (2.54)
для різних р, r1 і r2. Якщо деякі значення не ввійшли в таблиці, то можна використовувати співвідношення
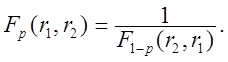 (2.55)
(2.55)
2.4 Оцінювання результатів спостережень над нормально розподіленою випадковою величиною
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.