Пример 5. Банк предлагает два вида облигаций сроком обращения каждая 2 года одинаковым номиналом. По одной из них начисляются простые проценты по ставке 24% годовых. Какова должна быть ставка сложных процентов по другой облигации, с тем, чтобы инвестор по истечении срока обращения получил тот же результат?
Решение:
Для расчета эквивалентной ставки сложных процентов воспользуемся формулой 14.
![]()
Ответ: эквивалентная ставка сложных процентов составит 21,65%.
Пример 6. Банк предлагает два вида сберегательных сертификатов. Срок обращения каждого составляет 2 года. По первому сертификату начисляются простые проценты по ставке 18% годовых. По второму начисляются сложные проценты из расчета 16% годовых. Какой сертификат является более выгодным для инвестора?
Решение:
Для решения задачи найдем простую ставку эквивалентную сложной и сравним полученный результат со значением простой ставки по первому сертификату или рассчитаем сложную ставку эквивалентную простой и сравним ее со значением сложной ставки, заданной по второму сертификату.
![]()
Так как заданное значение ставки по первому сертификату превышает расчетное значение эквивалентной ставки по второму сертификату, то можно сделать вывод о том, что первый сертификат обеспечивает инвестору больший уровень доходности, а, следовательно, является более выгодным.
![]()
Так как расчетное значение ставки меньше заданного по первому сертификату, то первый сертификат является более выгодным, так как обеспечивает инвестору больший уровень доходности.
Ответ: более выгодным с точки зрения инвестора является первый сертификат.
При начислении процентов m раз в году формулы эквивалентных ставок принимают следующий вид
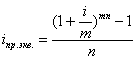 (15)
(15)
![]() (16)
(16)
Пример 7. Эмитент предлагает облигацию с возможностью разных условий начисления процентов. Первый вариант предусматривает начисление сложных процентов ежемесячно по ставке 2% на периоде. По второму варианту сложные проценты начисляются по полугодиям. По третьему варианту предлагаются простые проценты. Рассчитайте по второму и третьему вариантам ставки эквивалентные первому варианту.
Решение:
![]()
![]()
Ответ: по второму варианту эмитент должен предложить 25,22% годовых, а по третьему – 26,82% годовых.
4. Расчеты при обращении акций
Текущим доходом акционера выступает дивиденд, значение которого для привилегированных акций рассчитывается по формулам 1, 2, 5, 8. Выбор соответствующей формулы определяется видом ставки, применяемой эмитентом при расчетах дивидендов.
По обыкновенным акциям для расчета суммы дивиденда, приходящейся на одну акцию, применяется другая методика. Первым этапом решения задач подобного типа является расчет части чистого дохода, оставшегося после выплаты дивидендов по привилегированным акциям, приходящейся на одну обыкновенную акцию.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.