Лабораторная работа №3 “Идентификация параметров модели кинетики сложной химической реакции ”. 1
1. Постановка задачи регрессионного анализа. 1
2. Математический анонс. 1
Предварительная обработка результатов эксперимента. 2
Поиск оценок коэффициентов линейной регрессии. 3
Анализ остатков и выявление выбросов. 4
Проверка значимости влияния факторов на отклик. 4
Проверка адекватности регрессии. 5
3. Подготовка данных. 7
4. Рекомендации по реализации алгоритма регрессионного анализа данных в пакете STATISTICA. 7
5. Требования к оформлению лабораторной работы. 9
Цель работы. По результатам кинетического эксперимента, в котором варьировались концентрации исходных реагентов (Ci) и измерялась скорость химической реакции(W), идентифицировать параметры математической модели кинетики сложной химической реакции: константу скорости (k) и порядки реакции по компонентам (Ai). Модель имеет вид
W = k * C1A1 * C2A2 *. . . * CnAn , (1)
где: W - скорость химической реакции, Сi – концентрация i-го компонента, n - число компонентов.
Для идентификации параметров нелинейной математической модели кинетики химической реакции (1) следует путем логарифмирования представить её в виде линейной множественной регрессии
Ŷ = b0 + b1 * X1 + b2 * X2 + . . . + bn* Xn , (2)
где: Ŷ = ln(W) - отклик, Xi = ln(Ci) i = 1 . . . n - факторы, n - число факторов,
bi- коэффициенты, причем b0 = ln(k), bi = Ai , i = 1. . . n, .
Теперь поставленная в работе цель представляет собой задачу линейного регрессионного анализа. После решения этой задачи совершенно очевидно, что константа скорости реакции определится как экспонента от b0, а порядки реакции по компонентам - как соответствующие коэффициенты bi i = 1 . . . n.
При решении задач методами линейного регрессионного анализа принимаются следующие допущения:
· погрешность измерения факторов существенно меньше погрешности
измерения отклика, что позволяет считать факторы детерминированными величинами;
· погрешности измерения отклика имеют нормальное распределение;
· факторы x1 ,x2 ,....,xn независимые величины.
Обработка результатов эксперимента с целью получения регрессионной модели включает следующие этапы:
1. предварительная обработка результатов измерений;
2. поиск оценок коэффициентов линейной регрессии;
3. анализ остатков и выявление выбросов;
4. проверка значимости влияния факторов на отклик;
5. проверка адекватности регрессии.
Рассмотрим подробнее каждый из этих этапов при обработке результатов эксперимента уравнением линейной множественной регрессии вида (2).
Основная задача предварительной обработки результатов измерений состоит в оценке качества выполненного эксперимента, т.к. “плохой” эксперимент невозможно описать какой-либо регрессией с достаточной точностью. Для этого необходимо располагать результатами измерений отклика при одинаковых условиях, т.е. результатами параллельных опытов. По ним вычисляются средние значения отклика в каждом опыте
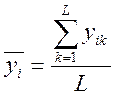 i=1, .... , m. (3)
i=1, .... , m. (3)
и дисперсии измерений отклика
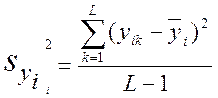 i=1, ... , m. (4).
i=1, ... , m. (4).
В
формулах (3) и (4): L - число параллельных опытов, m - число опытов. После расчета выборочных дисперсий
для всех опытов можно приступить к проверке их на равноточность. Оценка
равноточности выполняется по статистическому критерию Кохрена , который
используется для проверки нулевой гипотезы о равенстве генеральных дисперсий
измерения отклика во всех опытах H0 : 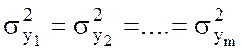 .
Критерий Кохрена рассчитывается
.
Критерий Кохрена рассчитывается
по формуле:
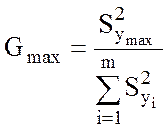 (5)
(5)
где
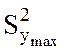 - максимальная дисперсия.
- максимальная дисперсия.
Это распределение зависит только от числа степеней свободы числителя (f1=L-1) и знаменателя (f2=m) . Проверка гипотезы H0 осуществляется по стандартной схеме:
1. задается уровень значимости p=0.05;
2. по таблице распределения Кохрена определяется квантиль G1-p(f1,f2) ;
3. если Gmax![]() G1-p(f1,f2),
гипотеза принимается, с вероятностью 0.95 можно
G1-p(f1,f2),
гипотеза принимается, с вероятностью 0.95 можно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.