считать, что опыты равноточны;
4. если Gmax > G1-p(f1,f2), гипотеза H0 отклоняется, при этом вероятность
ошибки первого рода 0.05.![]()
Для равноточных опытов можно вычислить среднюю дисперсию, которая называется дисперсией воспроизводимости и характеризует погрешность эксперимента
![]() S2воспр =
S2воспр =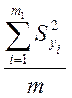 .
(6)
.
(6)
Еслиопыты неравноточны, экспериментальные данные не очень хорошего качества. В этом случае следует выявить опыты, выполненные с большой погрешностью. Для этого необходимо поочерёдно исключать опыты с максимальной дисперсией и каждый раз проверять оставшиеся опыты на равноточность, пока не будет выполнено условие равноточности. (В лабораторной работе исключение опытов с целью экономии времени можно не делать).
На этапе предварительной обработки целесообразно также оценить тесноту связи (корреляцию) между факторами и откликом. Для оценки используется корреляционная матрица, элементами которой являются коэффициенты парной корреляции. Чем больше абсолютная величина коэффициента, тем сильнее соответствующий фактор влияет на отклик. Знак коэффициента указывает на характер влияния: знак минус означает, что с увеличением фактора отклик уменьшается, а знак плюс означает, что с увеличением фактора отклик увеличивается.
Коэффициенты bi в регрессии (2) определяются методом наименьших квадратов из условия минимума Ф:
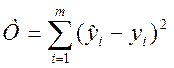 .
.
Если
в это выражение подставить ![]() в виде (2), то условием минимума функции Ф будетравенство нулю её частных производных по коэффициентам:
в виде (2), то условием минимума функции Ф будетравенство нулю её частных производных по коэффициентам:
¶Ф/¶b0 = 0, ¶Ф/¶b1 = 0, ¶Ф/¶b2 = 0, .... ¶Ф/¶bn = 0 . (7)
Выполнив дифференцирование, систему (2.13) можно представить в матричной форме:
X![]() XB
= X
XB
= X![]() Y,
(8)
Y,
(8)
где:
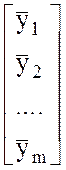
Y=![]()
 X=
X=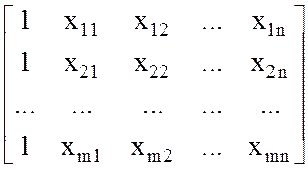 B=
B=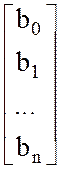
![]()
![]()
![]()
![]()
Y
– вектор
наблюдений, X – матрица факторов (единицы в первом столбце - значения
фиктивного фактора, который вводится для расчета коэффициента b0),
размерность матрицы m*(n+1).
B – вектор коэффициентов, X![]() - транспонированная
матрица факторов, размерность матрицы (n+1)*m, X
- транспонированная
матрица факторов, размерность матрицы (n+1)*m, X![]() X – информационная матрица, размерность
матрицы (n+1)*(n+1).
X – информационная матрица, размерность
матрицы (n+1)*(n+1).
Решение системы (8) относительно вектора B:
B= (X![]() X)-1 X
X)-1 X![]() Y
, (9)
Y
, (9)
где (X![]() X)-1 - обратная матрица.
X)-1 - обратная матрица.
Погрешность
расчета коэффициента bi: ![]() =
=
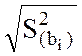 , i
= 0, 1,… n,
, i
= 0, 1,… n,
где:
![]() - выборочная оценка дисперсии
коэффициента регрессии bi, которая рассчитывается по
формуле
- выборочная оценка дисперсии
коэффициента регрессии bi, которая рассчитывается по
формуле
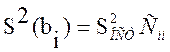 ,
(10)
,
(10)
![]() -
дисперсия
остатков, Cii– диагональный
элемент матрицы
-
дисперсия
остатков, Cii– диагональный
элемент матрицы ![]() .
.
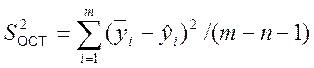 (11)
(11)
По величине остаткаri =![]() можно судить о точности представления
линейной моделью экспериментальных данных (см. математический анонс в разделе 2.1.3).
Остаток является величиной случайной. Известно, что в случае достаточно точной
модели остатки должны быть распределены по нормальному закону. Опыты, остатки
в которых нарушают нормальность распределения, являются выбросами и их следует
исключить из обработки, т.к. они искажают истинную картину регрессии. О
соответствии распределения остатков нормальному закону можно судить по правилу
двух сигм: все значения нормально распределенной величины с вероятностью 0.95
попадают в интервал [математическое ожидание
можно судить о точности представления
линейной моделью экспериментальных данных (см. математический анонс в разделе 2.1.3).
Остаток является величиной случайной. Известно, что в случае достаточно точной
модели остатки должны быть распределены по нормальному закону. Опыты, остатки
в которых нарушают нормальность распределения, являются выбросами и их следует
исключить из обработки, т.к. они искажают истинную картину регрессии. О
соответствии распределения остатков нормальному закону можно судить по правилу
двух сигм: все значения нормально распределенной величины с вероятностью 0.95
попадают в интервал [математическое ожидание ![]() 2σ], где σ –
стандартное отклонение. Математическое ожидание остатка равно нулю, в
качестве приближенного значения σ принимается выборочное отклонение Sост, которое определяется
по остаточной дисперсии
2σ], где σ –
стандартное отклонение. Математическое ожидание остатка равно нулю, в
качестве приближенного значения σ принимается выборочное отклонение Sост, которое определяется
по остаточной дисперсии ![]() :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.