Идентификация параметров модели кинетики сложной химической реакции, страница 4

 Примечание. При расчете степеней свободы  число опытов m и число факторов n берётся с учётомисключённых опытов и факторов.

·  В эксперименте отсутствуют параллельные опыты или не учитываются (способ, реализованный в статистических пакетах). В этом случае адекватность проверяют по коэффициенту детерминации (R²), который показывает насколько модель регрессии лучше модели среднего:

R² = 1 - 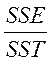                                                                   (15)

 - сумма квадратов, определяющая рассеяние экспериментальных значений отклика относительно  регрессии      =  ,

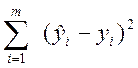 - сумма квадратов, определяющая рассеяние измерений отклика относительно среднего по всем опытам  ()

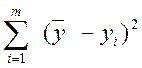  = ,           где              .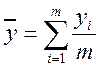

Если   ,  то  модель регрессии   представляет данные примерно с той же точностью, что и просто среднее и использовать регрессию не имеет смысла.  В этом случае 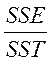 1 и   R² 0. 

Если   << ,  то регрессия представляет данные значительно точнее, чем  просто среднее и имеет смысл использовать регрессию. При этом 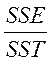 0  и  R²1.  Т.о.  чем ближе значение R² к 1, тем с большей уверенностью можно утверждать, что регрессия адекватна.  Коэффициент детерминации интерпретируют, как долю изменчивости отклика от факторов, объясняемую регрессией.  Например,  R² = 0.8   означает, что 80%  изменчивости Y от Xобъясняется регрессией, а  20% - случайностью.  В идеале желательно иметь объяснение если не для всей, то хотя бы для большей части исходной изменчивости.

Более строго предположение о значимости доли изменчивости, объясняемой  регрессией  можно проверить по критерию F:

                                                              

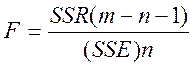
 - сумма квадратов, определяющая рассеяние среднего экспериментального значения отклика относительно  регрессии  

    =  .

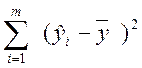Очевидно, что чем больше F, тем лучше регрессия описывает экспериментальные данные по сравнению со средним. Учитывая,     что

                               = + , 

F можно выразить  через  коэффициент детерминации

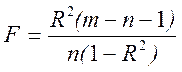                                                                                         (16)

Для рассчитанного значения  F по распределению Фишера можно вычислить уровень значимости p–level. Если  p–level < 0.05, то с вероятностью 0.95 можно признать   долю изменчивости, объясняемую  регрессией значимой и модель адекватной. В противном случае – изменчивость объясняется случайностью и полученная  регрессионная модель неприемлема.

Квадратный корень из коэффициента детерминации называется коэффициентом множественной корреляции R. R характеризует тесноту связи между факторами и откликом.

3. Подготовка данных

Данные подготовить в  файле сименем  kin242_№компьютера. Для  этого создать выборки из 30 элементов для следующих переменных:

C1

C2

WТ

W1

………

W5

С₁ – выборка из равномерного распределения в интервале 0.1 до 1.1;

С₂ - выборка из равномерного распределения в интервале 0.5 до 1.5.

                WT = k * C₁^A1  * C₂^A2              (k, A₁, A ₂ - из индивидуального задания).

   W₁,   W₂ ….  W₅  - нормально распределённые числа с математическим ожиданием WT и стандартным отклонением  -  5% от WT.

 Примечание: После генерации выборок все формулы сделать комментариями, для этого в поле формул в спецификации переменных  удалить знак равенства.

Индивидуальные задания.