Характеристики случайных процессов. Понятие случайной функции

1. ПОНЯТИЕ СЛУЧАЙНОЙ ФУНКЦИИ

          До определенных пор теория вероятностей ограничивалась понятием случайных величин. Их использование  позволяет выполнять статические расчеты, учитывающие случайные факторы. Однако механические системы подвергаются также разнообразным динамическим, то есть изменяющимся во времени воздействиям случайного характера. К ним относятся, в частности, вибрационные и ударные воздействия при движении транспортных средств, аэродинамические силы, вызванные атмосферной турбулентностью, сейсмические силы, нагрузки, обусловленные случайными отклонениями от номинальных режимов работы машин.

          Случайные динамические явления изучаются при анализе тенденций в экономике (например, изменения курса акций или валюты). Работа в условиях случайных возмущений характерна для систем управления разнообразными динамическими объектами.

          Для анализа подобных явлений используется понятие случайной функции. Случайной функцией X(t) называется такая функция аргумента t, значение которой при любом tявляется случайной величиной. Если аргумент принимает дискретные значения t₁, t₂, …, t_k то говорят о случайной последовательности X₁, X₂,…, X_k, где X_i = X(t_i).

          Во многих практических задачах неслучайный аргумент tимеет смысл времени, при этом случайную функцию называют случайным процессом, а случайную последовательность – временным рядом. Вместе с тем, аргумент случайной функции может иметь и иной смысл. Например, речь может идти о рельефе местности Z(x, y), где аргументами являются координаты местности x и y, а роль случайной функции играет высота над уровнем моря z. В дальнейшем, для определенности, имея в виду приложения случайных функций к исследованию динамических систем, будем говорить о случайных процессах.

          Предположим, что при исследовании случайного процесса X(t) произведено nнезависимых опытов, и получены реализации

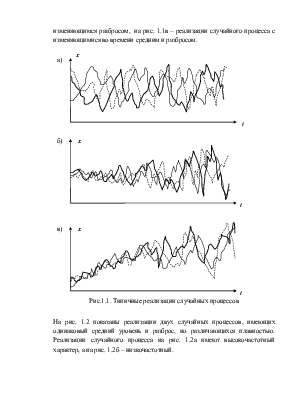
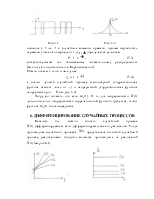
представляющие собой nдетерминированных функций. Соответствующее семейство кривых в определенной мере характеризует свойства случайного процесса. Так, на рис.1.1а представлены реализации случайного процесса с постоянными средним уровнем и разбросом значений возле среднего, на рис. 1.1б – реализации случайного процесса с постоянным средним и изменяющимся разбросом,  на рис. 1.1в – реализации случайного процесса с изменяющимися во времени средним и разбросом.

Рис.1.1. Типичные реализации случайных процессов

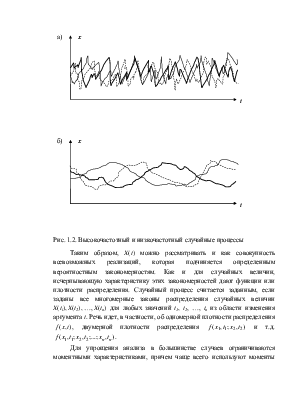
На рис. 1.2 показаны реализации двух случайных процессов, имеющих одинаковый средний уровень и разброс, но различающихся плавностью. Реализации случайного процесса на рис. 1.2а имеют высокочастотный характер, а на рис. 1.2б – низкочастотный.

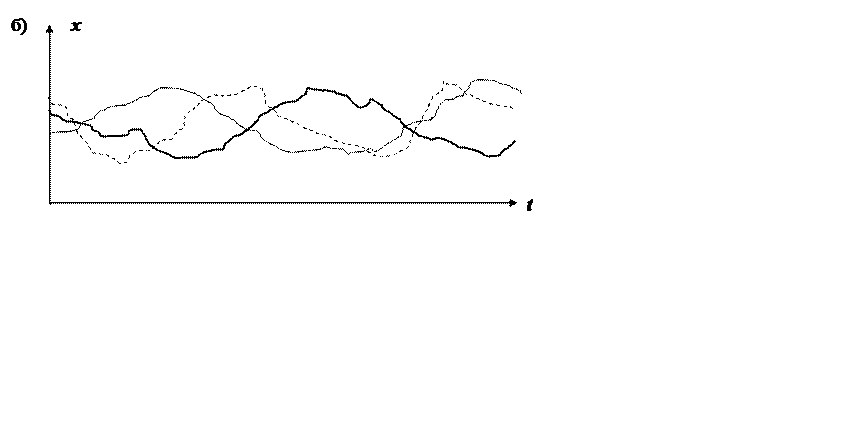
Рис. 1.2. Высокочастотный и низкочастотный случайные процессы

          Таким образом, X(t) можно рассматривать и как совокупность всевозможных реализаций, которая подчиняется определенным вероятностным закономерностям. Как и для случайных величин, исчерпывающую характеристику этих закономерностей дают функции или плотности распределения. Случайный процесс считается заданным, если заданы все многомерные законы распределения случайных величин X(t_i), X(t₂), …, X(t_n) для любых значений t₁, t₂, …, t_n из области изменения аргумента t. Речь идет, в частности, об одномерной плотности распределения , двумерной плотности распределения  и т.д. .

          Для упрощения анализа в большинстве случаев ограничиваются моментными характеристиками, причем чаще всего используют моменты первого и второго порядков. Для характеристики среднего уровня случайного процесса служит математическое ожидание

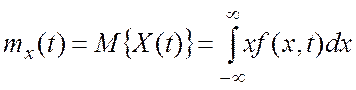                                .                                     (1.1)

          Для характеристики амплитуды отклонений случайного процесса от среднего уровня служит дисперсия

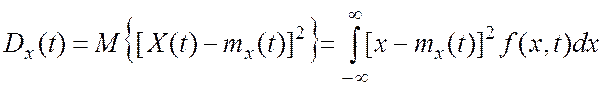                 .                 (1.2)

          Для характеристики изменчивости (плавности) случайного процесса служит корреляционная (автокорреляционная) функция

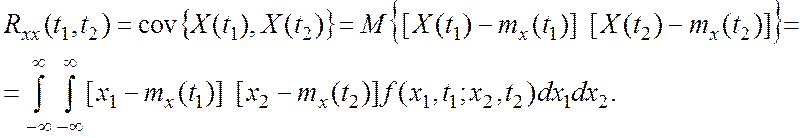       (1.3)

Как следует из (1.3), корреляционная функция представляет собой ковариацию случайных величин X(t₁) и X(t₂). Ковариация же, как известно из курса теории вероятностей, характеризует взаимозависимость между X(t₁) и X(t₂).

          В рамках корреляционной теории случайных функций, которая оперирует лишь моментами первого и второго порядков, могут быть решены многие технические задачи. В частности, могут быть определены априорная, а также условная вероятности выхода случайного процесса за пределы заданных границ. Вместе с тем, некоторые важные в практическом плане задачи не решаются средствами корреляционной теории и требуют использования многомерных плотностей распределения. К таким задачам относится, например, расчет среднего времени нахождения случайного процесса выше или ниже заданной границы.

2. ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ

2.1. Квазидетерминированные случайные процессы