Характеристики случайных процессов. Понятие случайной функции, страница 4

3. Возникающие в приложениях случайные процессы обычно могут быть представлены как результат действия на динамическую систему чисто случайных, т.е. некоррелированных случайных процессов. При всегда возможной дискретной аппроксимации такие непрерывные процессы могут быть представлены соответствующими случайными последовательностями, полученными на выходе динамических систем, описываемых разностными уравнениями, на вход которых подается ДБШ. Если речь идет о стационарных случайных процессах, то соответствующие разностные уравнения (так называемые формирующие фильтры) имеют постоянные коэффициенты и являются устойчивыми (то есть выход формирующего фильтра ограничен, если ограничен входной сигнал). Как и в примере  с марковской случайной последовательностью, решение разностного уравнения любого порядка может быть подобно (2.18) представлено в виде суммы двух составляющих, одна из которых зависит от начальных условий, а вторая - от будущих значений ДБШ, не зависящих от начальных условий. Рассмотрим два момента времени k и k+l и оценим корреляцию между x_k+l и x_k, Поскольку для устойчивой системы при  составляющая, зависящая от начальных условий в момент k, стремится к нулю /см.(2.18)/, то это значит, что  при . Аналогично в непрерывном варианте для стационарных случайных процессов

                                       .                               (3.8)

Таким образом, из свойств 1-3 следует, что график корреляционной функции стационарного случайного процесса:

1)  имеет максимум при   и укладывается в «трубку» ,

2)  симметричен относительно оси ординат,

3)  стремится к оси абсцисс при .

4)  график нормированной корреляционной функции при  имеет ординату, равную 1, и укладывается в «трубку» .

 

Рис.3.1. Графики нормированной и ненормированной корреляционной функции

4. Сходимость случайных последовательностей и процессов

Для анализа динамических систем, входными переменными которых являются случайные процессы, необходимо рассмотреть такие понятия, как непрерывность, производная и интеграл случайного процесса. Все эти понятия связаны с понятием предела, поэтому предварительно необходимо рассмотреть понятие сходимости к пределу случайной последовательности и случайного процесса.

А) Рассмотрим последовательность случайных величин  X_n ,      n=1,2,….

Определение 1. Случайная последовательность X_n, сходится к случайной величине X по вероятности, если для каждого

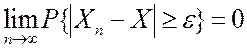                                       .                                              (4.1)

Определение 2. . Случайная последовательность x_n, сходится к случайной величине xв среднеквадратичном, если

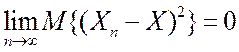                                       .                                               (4.2)

Свойства сходимости в среднеквадратичном

1.  Из сходимости в среднеквадратичном слкдует сходимость по вероятности. Это следует из неравенства Чебышева.

Действительно, обозначим . Тогда

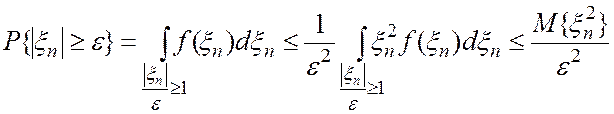                           (4.3)

Отсюда следует, что если 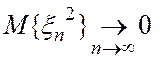 , то 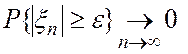, что и требовалось доказать.

Доказанное свойство полезно тем, что в рамках корреляционной теории легче бывает обосновать сходимость в среднеквадратичном.

2.  Возможен предельный переход под знаком математического ожидания :Теорема. Пусть для последовательности случайных величин X_n

                     в среднеквадратичном.

Тогда

                                   .                                (4.4)

1) Докажем, что         

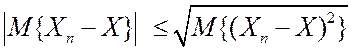                                   .                       (4.4’)

Действительно, дословно повторяя вывод (3.3), можно показать, что если есть случайные величины  , то

                                   .

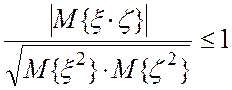В частном случае, при               

                                  

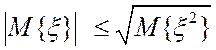
Тогда, полагая , получим (4.4’)

2) Из (4.4’), с учетом того, что , следует, что

                        .

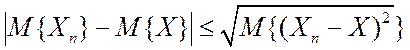Следовательно, если  при ,то

                             ,

что и доказывает (4.4).

Б) Рассмотрим случайный процесс X(t). Тогда говорят, что