Характеристики случайных процессов. Понятие случайной функции, страница 3

,                (2.12)

где  – любое число.

В частности,

                  и           .               (2.13)

          Для стационарных случайных процессов:

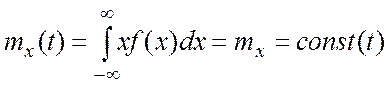                                  ,                             (2.14)

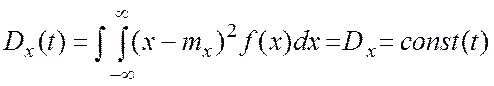                         ,                       (2.15)

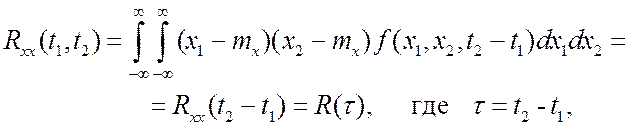                             (2.16)

т.е. математическое ожидание и дисперсия являются постоянными, а корреляционная функция зависит лишь от разницы аргументов.

Условия (2.14)-(2.16) – необходимые, но, вообще говоря, не достаточные условия стационарности. В силу (2.10) они являются достаточными лишь для стационарности нормальных случайных процессов.

          В теории случайных процессов вводится понятие стационарности в широком смысле, под которой подразумевается лишь соблюдение условий (2.14)-(2.16), а не условий (2.12).

2.3. Марковские случайные процессы

          Марковскими называются случайные процессы, закон распределения которых в будущий момент времени полностью определяется значением процесса в настоящий момент времени и не зависит от значений процесса в предыдущие моменты времени.

          Пример марковской случайной последовательности:

                                                                                                (2.17)

где  - так называемый дискретный “белый шум” (ДБШ), т.е. случайная последовательность, состоящая из не коррелированных друг с другом случайных величин, так что

                                   .

Действительно,

,

.                                                                           (2.18)

Поскольку  не зависят от  то из (2.18) следует, что вероятность появления тех или иных значений при фиксированном  не зависит от предшествующих  а значит последовательность (2.17) марковская.

3. СВОЙСТВА КОРРЕЛЯЦИОННОЙ ФУНКЦИИ

3.1 Общие свойства

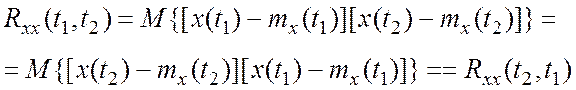1.                                    (3.1)

т.е. корреляционная функция – симметричная функция своих аргументов (поверхность  симметрична относительно биссектрисы ).

2. Введем понятие нормированной корреляционной функции

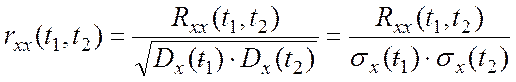                   .                            (3.2)

          Докажем, что

                                                .                                            (3.3)

          Действительно, поскольку

                   ,

то

                                                     

или                    

                          ,            

                                    ,

                                ,

                                               .

3.2. Свойства корреляционной функции для стационарных или стационарных в широком смысле случайных процессов:

1.                                 

                                   

Поскольку                  то

                                                                           (3.4)

т.е. корреляционная функция от стационарных случайных процессов четная.

2. Для стационарных случайных процессов

                                          

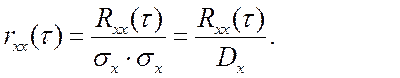
Поскольку   , то

                                                                                           (3.5)

Учитывая, что заключаем, что

                                                                                                          (3.6)

и                  .                                                                         (3.7)