К данному типу относятся случайные процессы, представляемые в виде неслучайной функции
![]() (2.1)
(2.1)
от t и нескольких случайных параметров, т. е. случайных величин С1, С2,…, Сn. Такой процесс полностью задается совместным законом распределения случайных параметров.
Пример 2.1.Случайная линейная зависимость
![]() .
(2.2)
.
(2.2)
Реализации данного случайного процесса представлены на рис. 2.1.
 |
Рис. 2.1. Реализации прямых со случайным наклоном и случайным смещением по вертикали.
Пример 2.2. Синусоида со случайной амплитудой и фазой
![]() . (2.3)
. (2.3)
Определим случайные параметры A и φ, решив систему уравнений
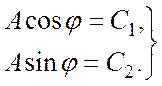
Тогда (2.3) можно записать в виде
![]() ,
,
где A и φ представляют собой случайную амплитуду и случайную фазу синусоидального сигнала с неслучайной частотой ω. Реализации этого случайного процесса представлены на рис. 2.2.
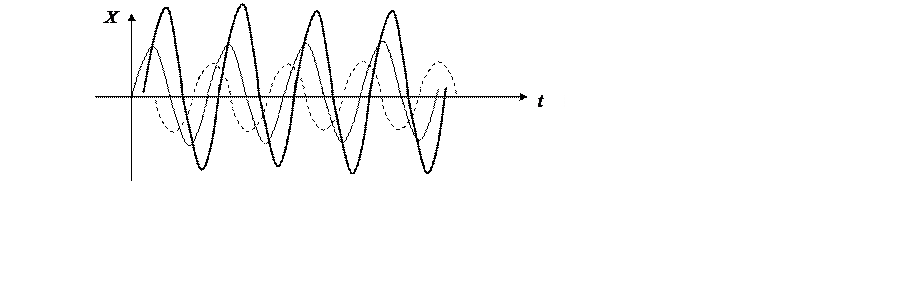
Рис. 2.2. Реализации синусоид со случайной фазой и амплитудой
Пример 2.3. Набор экспонент со случайными начальными условиями и случайными показателями

![]() .
.
Рис. 2.3. Реализации экспонент со случайными параметрами
Чаще всего рассматриваются линейные функции от случайных параметров
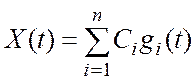 .
(2.5)
.
(2.5)
Реализацию процесса (2.5) можно
восстановить по замерам ее значений в nточках ![]() .
.
Если известны
математические ожидания ![]() и коэффициенты парной
корреляции
и коэффициенты парной
корреляции ![]() , то могут быть определены
, то могут быть определены ![]() и
и ![]() .
.
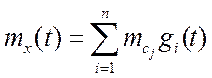 ,
(2.6)
,
(2.6)
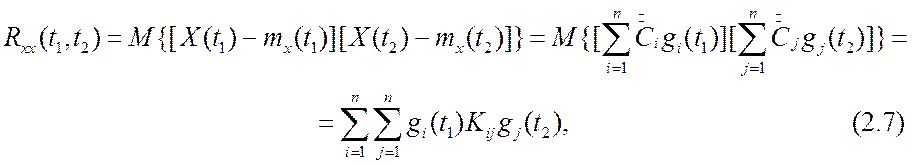 где
где 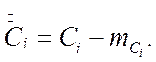
В частности,
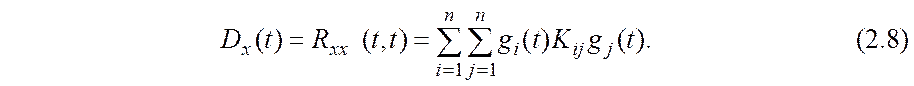 Пример
2.4. Зависимость пути от времени при случайных начальных условиях и
случайной скорости
Пример
2.4. Зависимость пути от времени при случайных начальных условиях и
случайной скорости
![]()
В этом случае для определения
корреляционной функции и дисперсии следует положить в (2.7) и (2.8) ![]()
Тогда получим
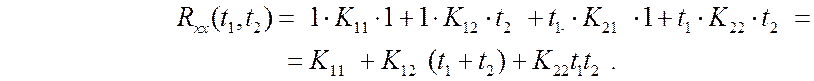
![]()
При ![]()
![]()
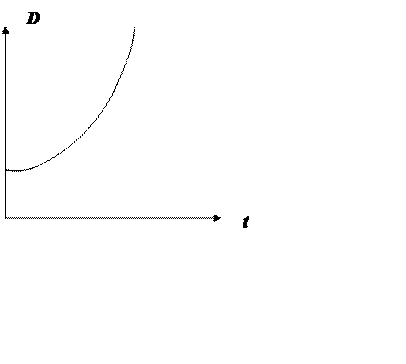
Рис.2.4. Зависимость дисперсии от времени
2.1. Нормальные случайные процессы
Случайный процесс называется нормальным (гауссовским), если все его распределения вероятностей
![]() нормальны
для любого n и любых ti.
нормальны
для любого n и любых ti.
Особая роль нормальных случайных процессов определяется тем, что:
1) в силу центральной предельной теоремы нормальное распределение встречается во многих прикладных задачах;
2) для нормального случайного процесса знания математического ожидания и корреляционной функции достаточно для определения любого распределения вероятностей типа (2.9)
Действительно, для n-мерной нормальной случайной величины (X1,X2,…,Xn) плотность совместного распределения имеет вид:
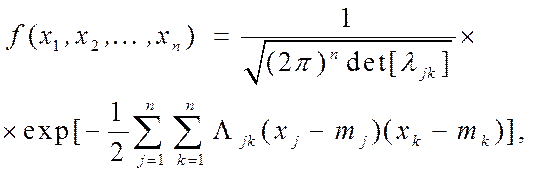 (2.10)
(2.10)
где
![]()
Здесь
![]()
коэффициент парной корреляции между xj и xk .
В частности, для .n=2
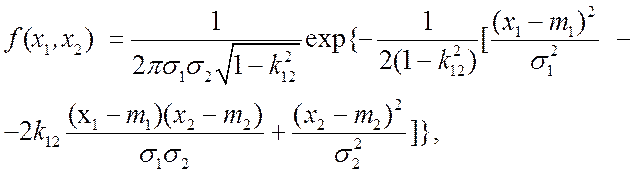 (2.11)
(2.11)
где
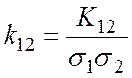 - нормированный коэффициент парной
корреляции;
- нормированный коэффициент парной
корреляции;
3) линейное преобразование нормальных случайных процессов (в частности, сумма или взвешенная сумма нескольких нормальных случайных процессов) есть нормальный случайный процесс (аналогично подобному свойству для нормальных случайных величин).
2.2. Стационарные случайные процессы
Если свойства случайного процесса не зависят от начала отсчета времени, то такие случайные процессы называются стационарными. В противном случае случайные процессы называются нестационарными.
Для стационарных случайных процессов все многомерные законы распределения зависят только от взаимного расположения моментов времени t1, t2, …, tn, то есть
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.