Характеристики случайных процессов. Понятие случайной функции, страница 6

На рис. 6.2 а) приведен пример недифференцируемого случайного процесса – поскольку первая производная его корреляционной функции терпит разрыв при , то она (первая производная) не дифференцируема в нуле, а это означает, что у корреляционной функции в нуле отсутствует вторая производная. На рис. 6.2 б) приведен пример дифференцируемого случайного процесса – у его корреляционной функции при  существуют и первая и вторая производные.

В рамках корреляционной теории случайных процессов свойства случайного процесса определяются его математическим ожиданием и корреляционной функцией .

Найдем вначале математическое ожидание производной.

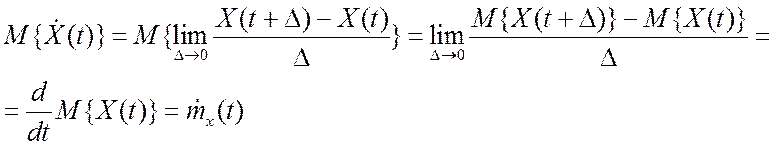       (6.4)

          Теперь определим корреляционную функцию производной.

Полагая вначале  центрированным процессом  (), найдем

 

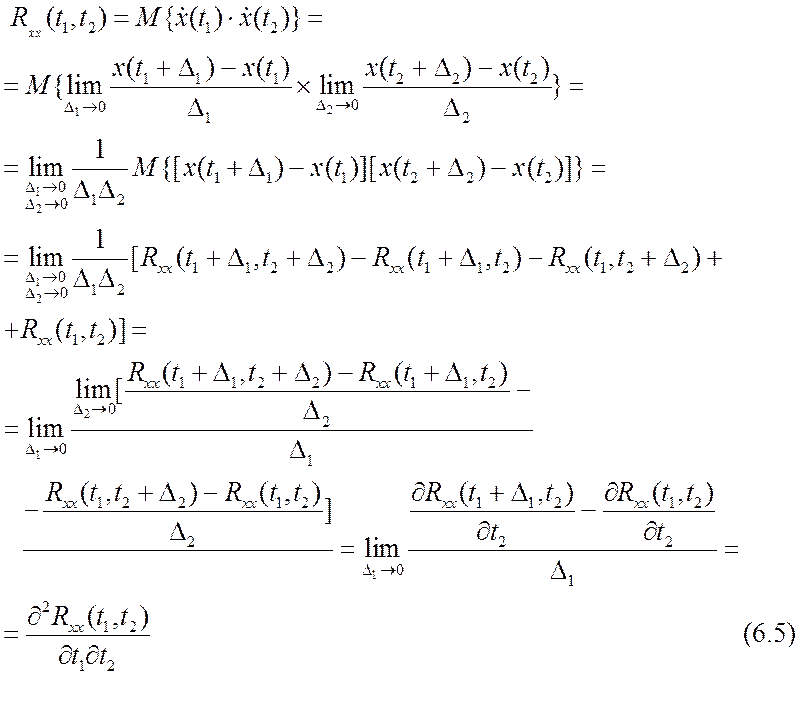
Для стационарного случайного процесса,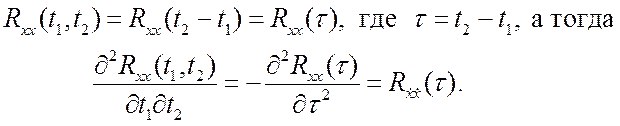

Таким образом, производная стационарного случайного процесса есть стационарный (в широком смысле) случайный процесс с характеристиками

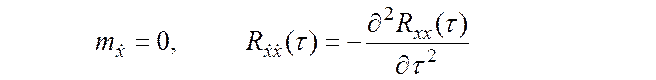                         (6.6)

Заметим, что хотя выражение для получено для центрированного процесса, оно сохраняет силу и в том случае, когда . Это связано с тем общим свойством, что корреляционная  функция не изменяется при добавлении к случайному процессу детерминированной функции.

Из (6.5) и (6.6) по индукции легко получить формулы для производных высших порядков

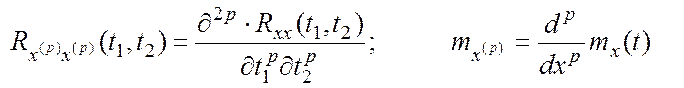                       (6.7)

и для стационарного случайного процесса

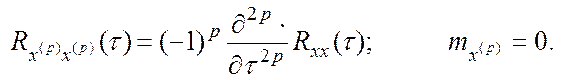                           (6.8)

7. ИНТЕГРИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ

Рассмотрим  интеграл от случайного процесса  вида

                                 

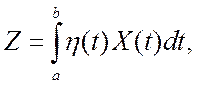
где  - неслучайная функция , а a и b - постоянные.

Под таким интегралом понимается, как и в обычном анализе, предел соответствующей интегральной суммы

,

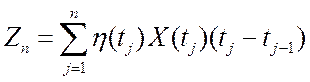где при  длина каждого интервала  стремится к 0, а предел понимается в смысле среднего квадратического.

Таким образом,

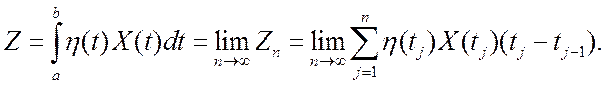                                   (7.1)

Данный интеграл Z представляет собой случайную величину, и в рамках корреляционной теории необходимо найти его математическое ожидание и дисперсию.

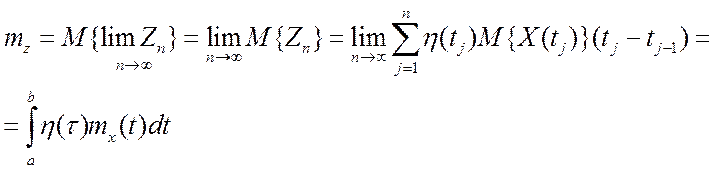            (7.2)

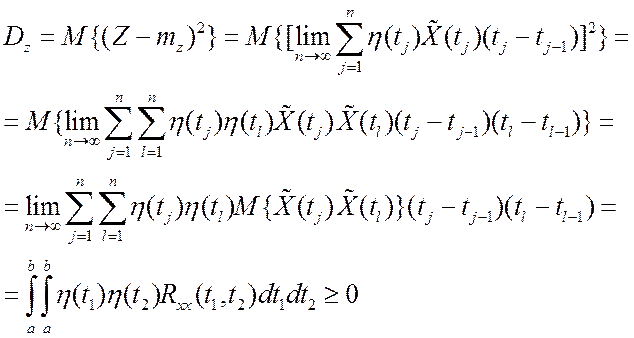                          (7.3)

Интегральное соотношение (7.3) должно выполняться для любой корреляционной функции при любых  Неравенство (7.3) накладывает определенные ограничения на вид корреляционной функции и может быть использовано для проверки пригодности различных аппроксимаций корреляционной функции.

          В приложениях часто фигурируют интегралы с переменным верхним пределом вида

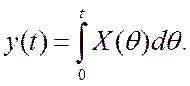                                                                                             (7.4)

Поскольку  - случайный процесс, то необходимо определить  и

          В соответствии с (7.2) при

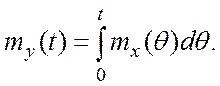                                                                                        (7.5)

Подобно выводу формулы (7.3)

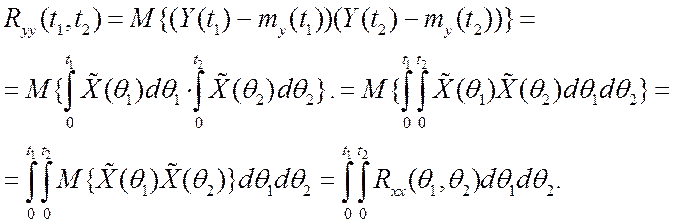                       (7.6)

В частном случае, когда интегрируемый случайный процесс стационарен,

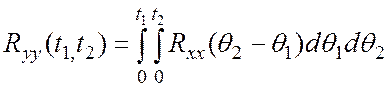                                                                (7..7)

и

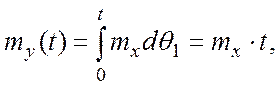                                                                                (7..8)

то есть интеграл от стационарного случайного процесса  - вообще говоря, нестационарный случайный процесс, так как  и  не обязано зависеть от .

Оказывается, (7.7) может быть упрощено сведением к однократному интегралу. Будем для определенности считать .

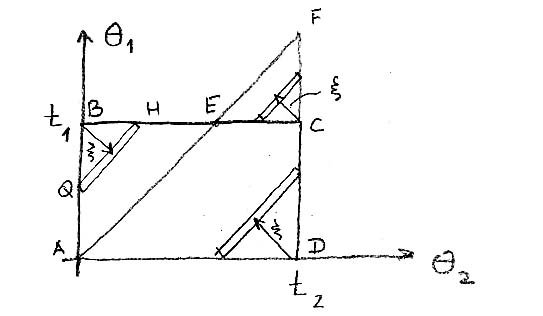
                                                            Рис.7.1.

Тогда

 

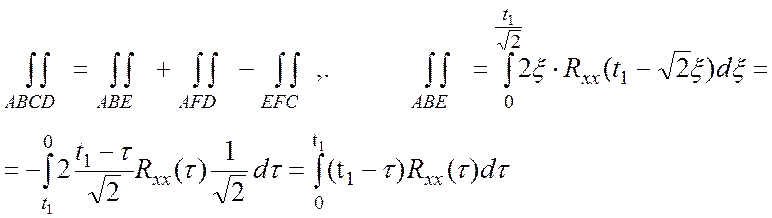
Аналогично

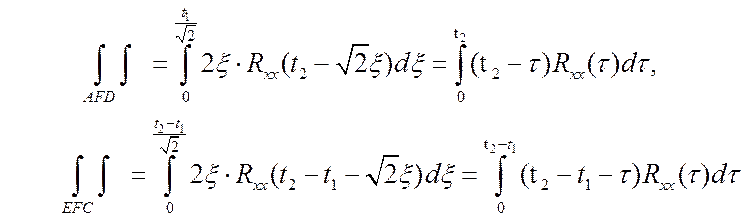
и

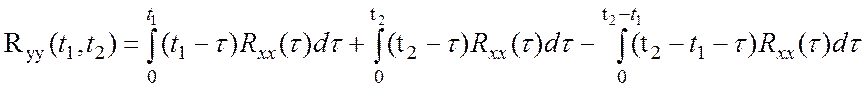
                                                                                                                     (7.9)

При 

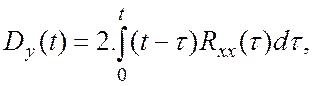                                                                        (7.10)

Более общей конструкцией, чем (7.4), является

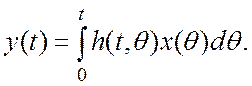                                                                                  (7.11)

Это так называемый интеграл свертки, определяющий выход динамической линейной системы y при подаче на ее вход воздействия x(t). Здесь  – весовая функция системы, определяющая ее реакцию в момент t на импульсное входное воздействие в момент .

В этом случае

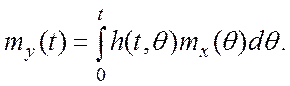                                                                            (7.12)

Для упрощения вывода выражения  можно считать . Тогда

       

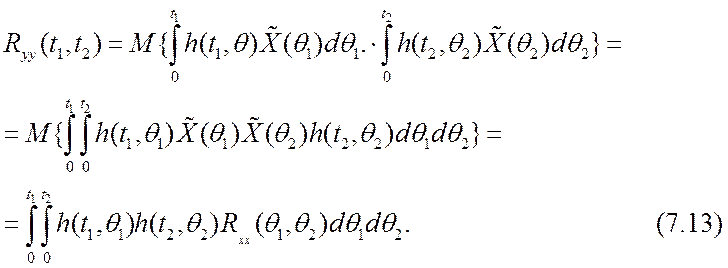
Таким образом, получены соотношения, принципиально решающие задачу анализа линейной динамической системы

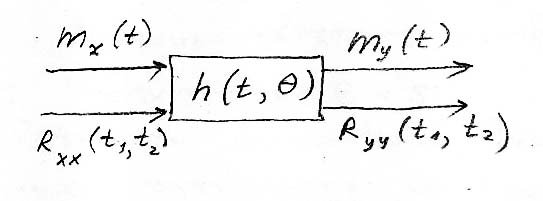
                                                       Рис.7.2.