Характеристики случайных процессов. Понятие случайной функции, страница 5

(X - случайная величина), если для любой последовательности значений аргумента  соответствующая случайная последовательность . При этом в зависимости от типа сходимости случайной последовательности  можно говорить о сходимости  либо по вероятности, либо в среднеквадратичном.

          В дальнейшем, используя аппарат корреляционной теории случайных процессов, будет удобнее говорить о сходимости в среднеквадратичном.

5. непрерывность случайных  процессов

Случайный процесс X(t) называется непрерывным, если

                                           .                                             (5.1)

          Рассмотрим для простоты центрированный случайный процесс с  и покажем, что для непрерывности случайного процесса в среднеквадратичном в (·)t достаточно непрерывности корреляционной функции этого процесса в (.)(t,t). Действительно,

          .        (5.2)

Если непрерывна при , то

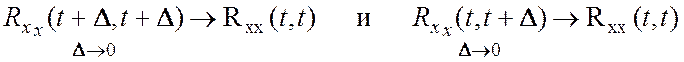, а значит к нулю стремится правая часть (5.2), откуда следует, что

                           при ,

 что и требовалось доказать.

Можно доказать, что если случайный процесс X(t) имеет ограниченную дисперсию , то условие непрерывности в (·) функции  является и необходимым для непрерывности [см. книгу Острема].

          Для стационарного случайного процесса   необходимым и достаточным условием непрерывности в среднеквадратичном является непрерывность  при .

          Обратим внимание на то, что непрерывность  в среднеквадратичном не означает, вообще говоря, непрерывность всех реализаций случайного процесса. В качестве примера может быть приведен так называемый телеграфный сигнал, который изменяет свое

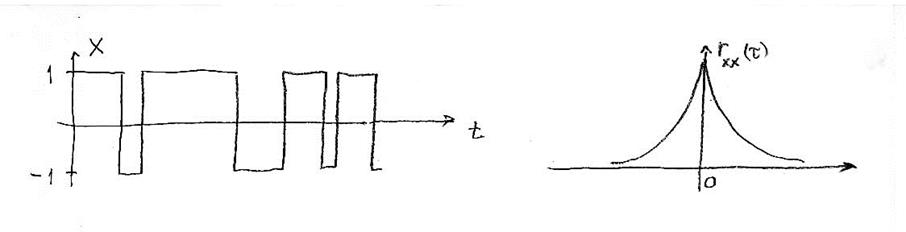
                          Рис.5.1                                                        Рис. 5.2

значение с 1 на –1 в случайные моменты времени, причем вероятность перемены знака на интервале от t до  определяется условием

                                                  ,                                                  (5.3)

соответствующим так называемому показательному распределению [cм.книгу Солодовникова или Первозванского].

Можно показать, что в этом случае

                                               ,                                                   (5.4)

а значит данный случайный процесс стационарный (корреляционная функция зависит лишь от ) и непрерывный (корреляционная функция непрерывна при , см. рис. 5.2).

          Нетрудно показать, что если , то для непрерывности  дополнительно к непрерывности корреляционной функции требуется, чтобы функция  была непрерывна.

6. Дифференцирование случайных  процессов

          Казалось бы, можно считать случайный процесс дифференцируемым, если дифференцируемы все его реализации. Тогда производная случайного процесса  представляла бы собой случайный процесс, реализациями которого являются производные от реализаций 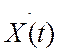(см.рис 6.1).

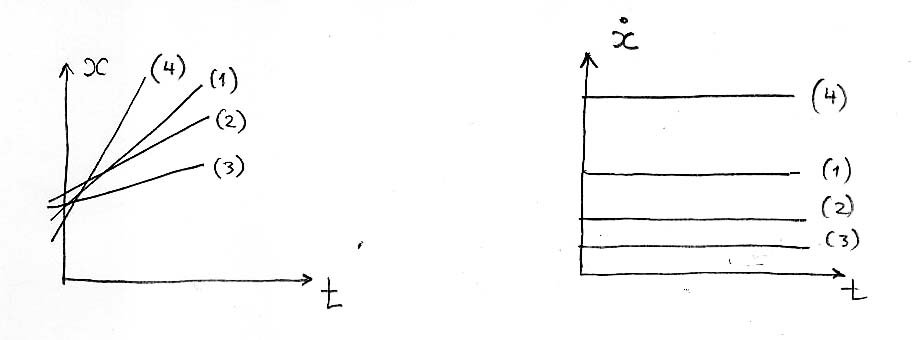
                                                            Рис.6.1.

При таком определении у всех реализаций должна существовать производная. Однако в корреляционной теории случайных процессов дается более общее определение дифференцируемости, не требующее дифференцируемости каждой реализации, а именно:

  является производной  в (·) t, если

                                       

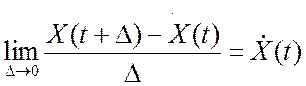
существует в смысле среднеквадратичной сходимости, т.е. если

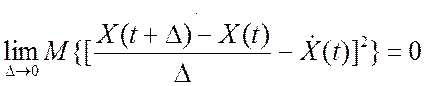                               .                             (6.1)

Теорема. Случайный процесс  с ограниченной дисперсией дифференцируем в среднеквадратическом тогда и только тогда, когда функция  дифференцируема в (·) t и существует смешанная вторая производная от корреляционной функции

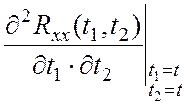                                                                                               (6.2)

[Для любознательных - доказательство в книгах Острема, Свешникова].

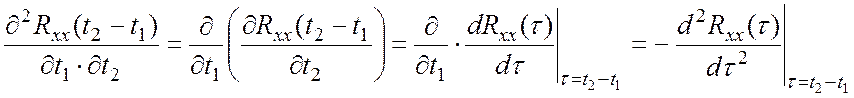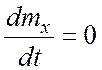В частном случае стационарного случайного процесса , так как  и

а тогда

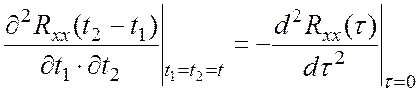                            .                              (6.3)

Таким образом, для дифференцируемости стационарного случайного процесса необходимо и достаточно существование второй производной  корреляционной функции при .

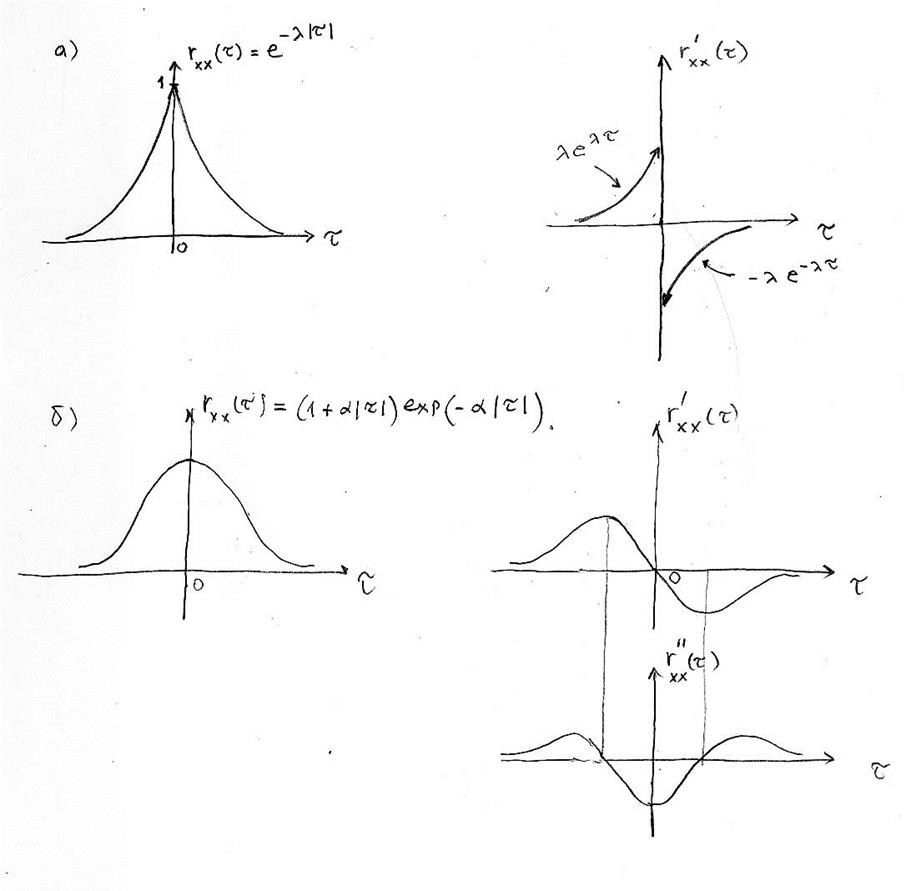
Рис. 6.2