Отражение волн. Преломление волн. Использование отражения света. Прохождение света через прозрачную трёхгранную призму, плоско-параллельную пластинку. Линзы. Оптические приборы, страница 27

В предыдущем параграфе было показано, что положение изображения S1 однозначно определяется положением самой светящейся точки S относительно линзы. Поэтому точки S и S1 называют сопряжёнными точками линзы. Выведем формулу сопряжённых  точек линзы, позволяющую находить положение изображения S1 с помощью вычислений.

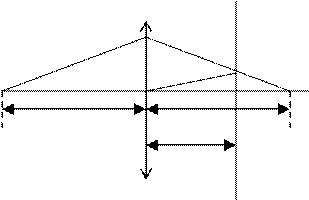
Пусть на главной оптической оси собирающей линзы с оптическим центром О и фокусами Ф1 и Ф2 находится светящаяся точка S (рис. 16), изображение которой получилась в точке S1. Напомним, что КМ-фокальная плоскость линзы, а ОА1║ SА. Обозначим расстояние от светящейся точки S до оптического центра О-через f(OS1=f) и главное фокусное расстояние - через F(OФ1=F). На подобии треугольников SAS1 и OA1S1 (ОА1║SA) имеем:

                                                     SS1\OS1=AS1\A1S1, или  (d+f)\f=AS1\A1S1. Из подобия треугольников  ОАS1 и  ФА1 S1 можно написать

                                                     OS1\Ф1S1=AS1\A1S1, или f\(f-F)=AS1\A1S1 

поскольку  правые части найденных пропорций равны, получаем

                                                     (d+f)\f=f\(f-F), откуда fF+dF=df.

После деления обеих частей этого неравенства на dfF получим формулу сопряжённых точек линзы:

                                                              1\d+1\f=1\F. Формула 3.

 Так как справа стоит оптическая сила линзы, имеем

                                                              1\d+1\f=D. Формула 4.

                                                  М                                    d                                                        d

                                 А                                                                                                              

                                                       А1

      S                Ф2                                                     О   S         S1                                О              S           S1

                    d                        f        Ф1      S1

                                            F

                                                                                             d                                                                                              f

(б)

(а)

                                                                            

                                                  К

Рисунок 17 – мнимое изображение в линзе

                          

Из формулы 3 видно, что от перемены местами значений  d и f формула не изменяется. Это означает, что светящаяся точка и её изображение в линзе переместимы, т.е. если светящуюся точку переместить туда, где было её изображение, то изображение получится там, где была светящаяся точка. Именно поэтому точки S и S1 называют сопряжёнными. Следует запомнить, что соотношения (формула 3) и (формула 4) применимы как собирающим, так и к рассеивающим линзам. При расчётах значения  действительных величин всегда подставляются со знаком плюс, а мнимых - со знаком минус.  Например, для рассеивающей линзы на место F или D ставится число со знаком минус. Отрицательный ответ, полученный в результате вычислений, показывает, что соответствующая ему величина мнимая.

Напомним, что светящаяся точка S тоже может быть мнимой. На рис.17,а, показан  мнимый источник света S и его действительное  изображение в собирающей линзе S1, а на рис.17,б,- мнимый источник света S и его действительное изображение S1 в рассеивающей линзе.

7. Построение изображения светящейся точки, расположенной на побочной оптической оси линзы.   

Когда светящаяся точка S находится на побочной оптической оси линзы, то линза создаёт её изображение на той же оси. Выясним, как строится это изображение.