Примеры
изображения предметов, создаваемых сферическими зеркалами, показаны на рис.14.
Заметим, что выпуклое зеркало всегда даёт мнимое изображение предметов. Выясним,
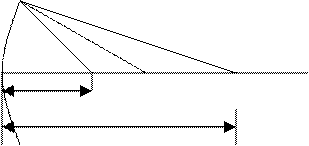
как найти положение светящейся точки А, расположенной на главной оптической оси
ОС зеркала. (рис.15). Ясно, что изображение точки должно быть на этой же оси. Проведём
из точки А произвольный луч АВ. В точку его падения В проведём радиус СВ. Он
является нормалью (перпендикуляром) к поверхности зеркала, поэтому угол 1= углу
2, что и определяет положение отраженного луча ВА1. В точке А1 и получится
изображение точки А. Положение точки А1 однозначно определяется положением
самой точки А. Поэтому точки А и А1 называют сопряжёнными.
А
А
Ф В1
С А1
В
С Ф
А1 В1 В
Обозначим расстояние АО через d,
А1О- через f и ОС- через R. Для зеркал, поверхность
которых составляет малую часть поверхности сферы, приближённо можно считать,
что ВА≈ОА≈d и ВА1≈ОА1≈f. Так как угол 1=углу 2, то
линия ВС в треугольнике АВА1, является биссектрисой угла АВА1, а это означает,
что отрезки АС и А1С пропорциональны сторонам треугольника АВА1:
АС1\АС=ВА1\ВА,
или (R-f)\(d-R)=f\d
Преобразуем последнее соотношение:
Rd-fd=fd-Rf; Rf+Rd=2fd. После деления на Rfd
получим 1\d+1\f=2\R.
Заменяя R его значением,
получим формулу сопряжённых точек зеркала:
1\d+1\f=1\F -
формула 2.
Эта формула справедлива как
для вогнутых, так и для выпуклых зеркал, но числовые значения действительных
величин следует подставлять с плюсом, а мнимых - с минусом. Например, главное
фокусное расстояние вогнутых зеркал берётся со знаком плюс, а выпуклых - со
знаком минус. Отрицательный ответ показывает, что соответствующая ему
величина- мнимая.
6. Законы преломления
света.
