С помощью оптической шайбы можно показать, что падающий и отражённый лучи обратимы, т.е. если падающий луч направить по пути отражённого луча, то отражённый луч пойдёт по пути падающего луча.
В одном из предыдущих пунктов были установлены законы отражения для сферического фронта волны. Покажем теперь, что они справедливы и для плоского фронта волны, т.е. для случая падения на плоскую поверхность параллельных лучей. Пусть на гладкую поверхность КМ (Рис.3) падает плоская волна, фронт которой в какой-либо момент времени занимает положение А1В1. Через некоторое время он займёт положение АС. В этот момент времени (мы примем его за нуль) от точки А начнёт распространяться элементарная волна. Пока фронт волны за время t из точки С переместится в точку В, волна из точки А распространится в точку В, волна из точки А распространится по полусфере на расстояние АД, равное СВ, т.к. АД=vt и СВ=vt (v-скорость распространения волн). Новым положением фронта волны после отражения лучей будет касательная к полусфере, проведённая из точки В, т.е.прямая ВД. Дальше этот фронт волны будет двигаться параллельно самому себе по направлению лучей АА11и ВВ11. Поскольку прямоугольные треугольники АДС и АСВ имеют общую гипотенузу АВ и равные катеты АД и СВ, то они равны между собой. Поэтому угол ί1= углу α1. Так как угол ί1= углу ί и угол α1= углу α как углы со взаимно перпендикулярными сторонами, то и угол α=углу ί, т.е. угол падения равен углу отражения, что и требовалось доказать.
2. Зеркальное и диффузное отражения. Плоское зеркало.
Когда отражение света происходит от неровной поверхности, то ход отражённого луча в каждой его точке определяется следующим образом. В точке падения луча проводится плоскость, касательная к поверхности, от которой происходит отражение, а за тем строятся углы падения и отражения по отношению к этой плоскости.
|
|
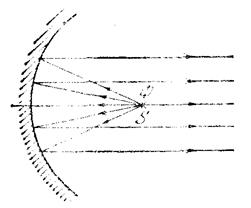
Таким способом определены направления отражения лучей в различных точках поверхности на рис.4, где видно, что лучи, которые до отражения шли параллельным пучком, после отражения идут в разных направлениях. Такое отражение света происходит от всех шероховатых поверхностей. Рассеянный свет, идущий от поверхностей различных тел, позволяет нам видеть эти тела. Идеально гладкую поверхность, хорошо отражающую свет, называют зеркальной. Плоская зеркальная поверхность является плоским зеркалом( кроме плоских зеркал бывают сферические, параболические и т.п.) Пучок параллельных лучей после отражения от плоского зеркала остаётся параллельным, но изменяет направление своего распространения (рис.5.). Такое отражение называют зеркальным или правильным. На практике зеркальное отражение получается, если размеры неровности на поверхности не превышают длины волны светового излучения. Когда световые лучи от сильного источника света после отражения от плоского зеркала попадают в глаз человека, то они ослепляют его. Диффузное отражение неприятных ощущений в глазу не вызывает.
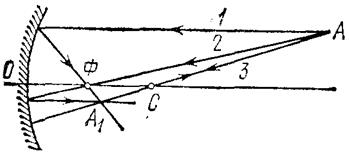
Если свет, рассеянный поверхностями различных тел, попадает на плоское зеркало, а затем, отражаясь, попадает в глаз человека, то в зеркале видны изображения этих тел.Выясним, как они возникают. Сначала рассмотрим, получается изображение одной светящейся точки в плоском зеркале.
Пусть над поверхностью зеркала КМ(рис.6) находится точечный источник света S. Луч SA, который идёт от источника Sпо перпендикуляру к зеркалу, после отражения меняет своё направление на противоположное, т.е. идёт по пути АS. Из всего множества лучей, падающих из S на зеркало, выделим луч SB, который падает на зеркало под углом ί. После отражения он идет по пути ВД, причём угол α=углу ί. На рис.6. видно, что лучи, падающие в точки А и В, после отражения идут так, как будто бы они вышли из одной точки S1, расположенной симметрично точке S относительно зеркала КМ. Докажем это.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.