Гидромеханический амортизатор. Назначение, краткая характеристика. Анализ условий и режима эксплуатации, страница 14

Интервал, ч	Середина интервала, ti, ч	Частота ni	Опытная вероятность pi=ni/n	F(t)=S(ni/n)	f(t)=pi/Dt
104-117 117-130 130-143 143-156 156-169 169-182 182-195 195-208 208-221 221-234 234-247 247-260 260-273	111 124 137 150 163 176 189 202 215 228 241 254 267	4 12 9 11 12 10 16 17 17 14 12 9 1	0,028 0,083 0,063 0,076 0,083 0,069 0,111 0,118 0,118 0,097 0,083 0,063 0,007	0,028 0,111 0,174 0,25 0,333 0,402 0,513 0,631 0,749 0,846 0,929 0,992 1	0,002 0,0064 0,005 0,0058 0,0064 0,005 0,0085 0,009 0,009 0,007 0,006 0,005 0,001

Определим среднее значение для статистического ряда:

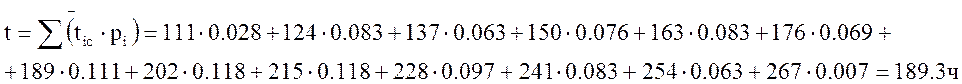
Определим среднее квадратичное отклонение:

Оределим коэффициент вариации:

;

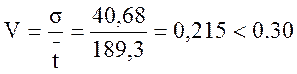Рекомендуется в первом приближении принимать распределение по нормальному закону распределения.

Строим теоретические кривые функции плотности распределения наработки f(t), теоретическую вероятность безотказной работы P(t), теоретическую функцию распределения отказности F(t) и функцию интенсивности отказов l(t). Для этого найдем эти значения.

Вычислим значения функции плотности распределения наработки f(t),

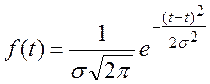
Вычислим значения теоретической вероятности безотказной работы P(t)  на каждом интервале по формуле:

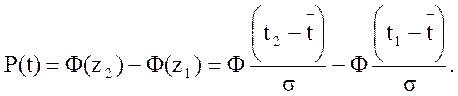
Вычислим значения теоретической функции распределения отказности F(t) по формуле:

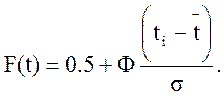
Вычислим значения  функции интенсивности отказов по формуле:

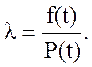
Все полученные значения заносим в таблицу 8.2

Таблица 8.2

Интервал,ч
111 124 137 150 163 176 189 202 215 228 241 254 267	0,0015 0,0027 0,0043 0,0061 0,0078 0,0093 0,0098 0,0093 0,008 0,0062 0,0044 0,0028 0,0016	0,973 0,945 0,901 0,834 0,742 0,629 0,504 0,378 0,264 0,171 0,102 0,056 0,028	0,027 0,055 0,099 0,166 0,258 0,371 0,496 0,622 0,736 0,829 0,898 0,944 0,972	0,0015 0,0029 0,0048 0,0073 0,0105 0,0148 0,0194 0,0246 0,0303 0,0363 0,0431 0,05 0,0571

Проверим гипотезу по критериям согласия о правильности выбранного закона

Критерий Пирсона: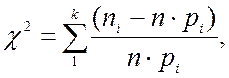

где k – число интервалов статистического ряда;

n_i – частота в i-ом интервале;

n – общее число значений случайной величины;

p_i – теоретическая вероятность попадания случайной величины в iом интервале

p_i=p_iн-p_ik, где p_iн  и p_ik – функция вероятности в конце и в начале i-го интервала.

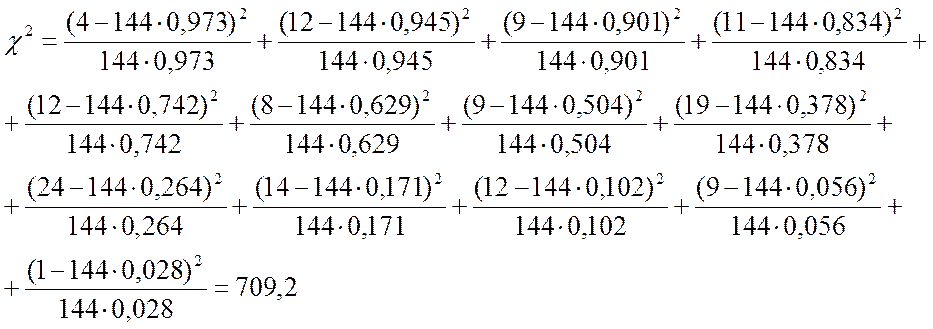
Число степеней свободы r=k–s=13–3=10. При r=10 и c²=709,2 [6] вероятность совпадения теоретического и статического распределения Р=0,15<0,1 ,  что не подтверждает принятую нами гипотезу о распределении наработки гидромеханического амортизатора (ГНАД-195) до отказа по нормальному закону распределения.

Критерий Колмогорова. Значение вероятности попадания случайной величины приведено в таблице 8.3

Гистограмма 1

 

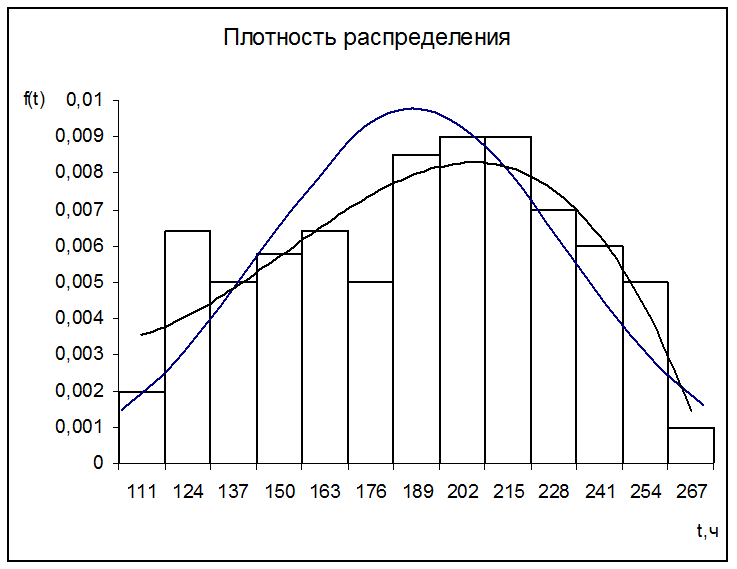
Таблица 8.3 – Значение вероятности попадания случайной величины

t, ч	P(t)теор	Pi	F(t)теор	F(t)опытн	½D½=F(t)т-F(t)o
111 124 137 150 163 176 189 202 215 228 241 254 267	0,973 0,945 0,901 0,834 0,742 0,629 0,504 0,378 0,264 0,171 0,102 0,056 0,028	0,028 0,083 0,063 0,076 0,083 0,069 0,111 0,118 0,118 0,097 0,083 0,063 0,007	0,027 0,055 0,099 0,166 0,258 0,371 0,496 0,622 0,736 0,829 0,898 0,944 0,972	0,028 0,111 0,174 0,25 0,333 0,402 0,513 0,631 0,749 0,846 0,929 0,992 1	0,001 0,056 0,075 0,084 0,075 0,031 0,017 0,009 0,013 0,017 0,031 0,048 0,028

Из таблицы 8.3 следует, что ½D_max½=0,084, тогда параметр распределения l=D_max=0,084∙12=1,008.

По таблице 10 [3] находим Р(l)=0,27 т.е. гипотеза о распределении по нормальному закону распределения.