Гидромеханический амортизатор. Назначение, краткая характеристика. Анализ условий и режима эксплуатации, страница 13

Рисунок 7.1- Расчетная схема корпуса амортизатора  

Найдем значения радиальных напряжений:

,                                                       

где давление промывочной жидкости, МПа;

наружный соответственно внутренний радиусы корпуса, .

МПа

Найдем значение тангенциальных напряжений:

МПа

Условие прочности корпуса имеет вид:

, где - допускаемое напряжение при расчете на внутреннее давление, 210 МПа.

Найдем величину  по третей теории прочности:

МПа

условие прочности выполняется

8  ОБРАБОТКА  ИНФОРМАЦИИ О НАДЁЖНОСТИ                 АМОРТИЗАТОРА ГИДРОМЕХАНИЧЕСКОГО

Нагрузки, действующие на детали, агрегаты буровых и нефтегазопромысловых машин во время эксплуатации носят случайный характер. Случайными являются также характеристики материалов, конкретное значение которых зависит от множества факторов. Примерами случайной величины являются наработка на отказ, интенсивность отказов, технический ресурс, срок службы машины. Случайной величиной называется величина, которая в результате испытаний может принять значение, причём нельзя заранее предсказать, какое именно. Совокупность значений случайных величин, расположенных в возрастающем порядке с указанием вероятностей их появления, называют распределением случайных величин. Соотношения, устанавливающие связь между возможными значениями случайной величины и соответствующими им вероятностями, называют законом распределения.

Статическая информация о наработке до отказа за гидромеханического амортизатора-диспергатора (ГНАД-195) в часах по данным Нефтекамского УБР:

112	114	114	116	117	117	118	120	122	123	124	125
125	125	127	127	127	128	129	129	130	139	140	142
143	143	144	145	146	148	150	151	153	153	154	156
156	157	158	158	162	163	163	165	166	168	168	169
171	173	174	177	177	179	180	183	183	184	185	187
187	190	192	194	195	195	196	197	197	198	199	199
201	202	202	203	204	204	205	205	206	207	207	208
208	209	209	210	210	211	211	212	212	213	213	214
214	215	215	216	216	217	217	218	219	220	220	221
221	223	224	224	225	225	227	228	230	232	232	232
233	233	234	236	236	238	238	239	240	240	241	244
244	245	246	246	248	256	257	258	264	266	267	268
n=144

Найдем число интервалов:

k=.

Определим величину одного интервала:

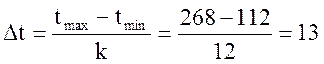,ч где t_max, t_min – соответственно наибольшее и наименьшее значения случайной величины.

При составлении статистического ряда для каждого интервала подсчитывают:

n_i – количество значений случайной величины в i-ом интервале;

p_i=n_i/n – частность (опытная вероятность) в i-ом интервале;

f(t)=p_i/Dt – эмпирическую плотность вероятности;

F(t)=S(n_i/n) – эмпирическую вероятность отказов.

Таким образом, строим статистический ряд представленный в таблице 8.1.

Таблица 8.1 – Статистический ряд