Дифференциальные уравнения и передаточные функции звеньев САУ. Линеаризация нелинейных статических характеристик и нелинейных уравнений. Составление и преобразование структурных схем САУ. ТАУ. Часть 1: Методические материалы и указания к практическим занятиям, страница 8

U_в, I_в – напряжение и ток возбуждения генератора.

ЭМУ. Если нагрузкой ЭМУ является цепь возбуждения генератора, то дифференциальное уравнение имеет вид:

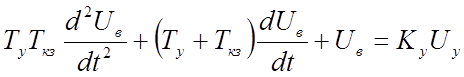,                (63)

где Т_у, Т_кз – постоянные времени цепи управления и К.З. цепи;

К_у – коэффициент передачи ЭМУ по напряжению.

Электронный усилитель. Уравнение усилителя (Т_эу=0):

,                                (64)

где К_эу – коэффициент усиления электронного усилителя.

Тахогенератор. Уравнение ЭДС якоря тахогенератора:

,                                     (65)

где К_ТГ – коэффициент передачи тахогенератора.

Уравнение (60) – (65) определяют динамический режим работы системы после появления внешнего воздействия.

Запишем уравнение (60) – (65) в операторной форме:

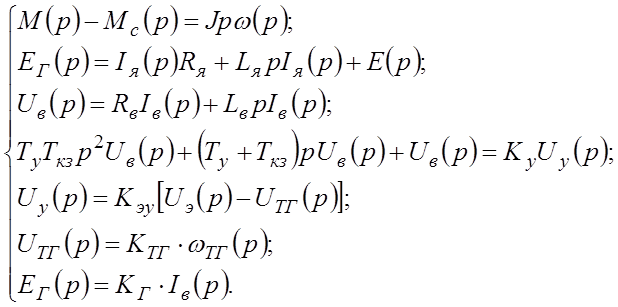             (66)

Преобразуем систему (66, принимая во внимание: М=КФI_я, М_с=КФI_с, Е=КФw:

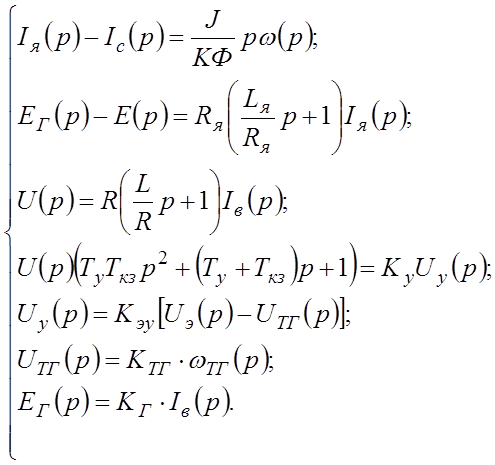                       (67)

Обозначив: , ; ,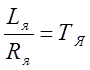

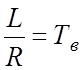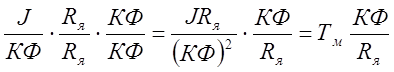где ,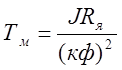

получим:

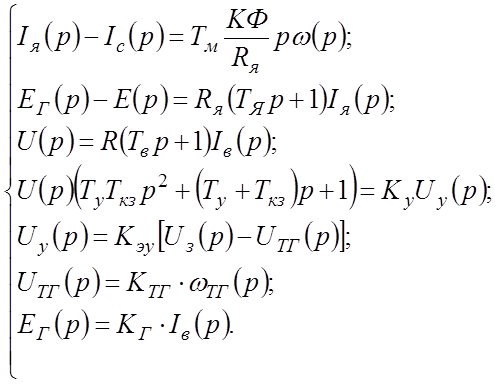                      (68)

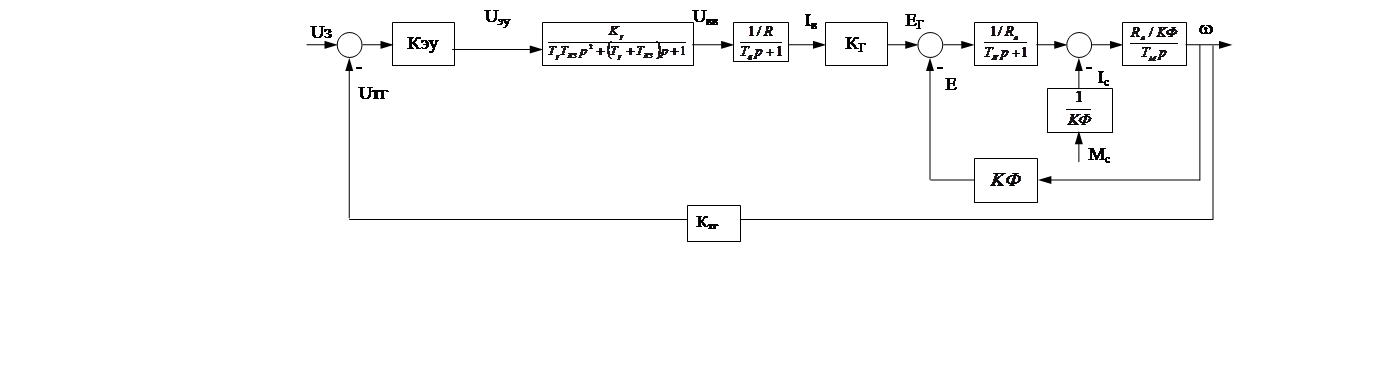
Используя полученную систему уравнений, составим структурную схему представленную на рисунке 11.

3.2  Преобразование Структурных схем (Алгебра блочных схем)

Для упрощения структурных схем, получения передаточных функций разомкнутой и замкнутой систем по управляющему, по возмущающему воздействию и по ошибке применяются структурные преобразования. Структурные преобразования основаны на принципе суперпозиции и поэтому применимы только для линейных систем. Довольно часто в результате структурных преобразований удаётся привести исходную многоконтурную систему к простейшей одноконтурной.

Основные правила преобразования структурных схем:

1. Несколько последовательно соединённых звеньев (рисунок 12) можно заменить одним звеном с передаточной функцией  равной произведению передаточных функций этих звеньев:

.           

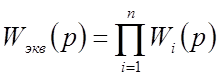                       (69)

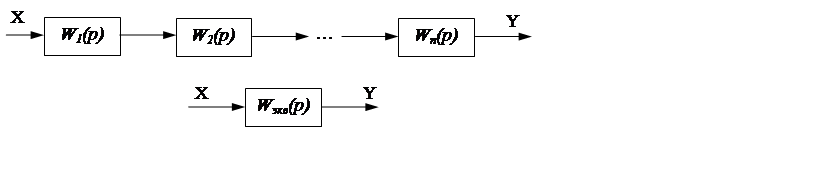
Рисунок 12.  Последовательное соединение звеньев

2. Несколько параллельных соединенных звеньев (рисунок 13) можно заменить одним с передаточной функцией,  равной сумме передаточных функций звеньев:

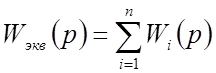.                                       (70)

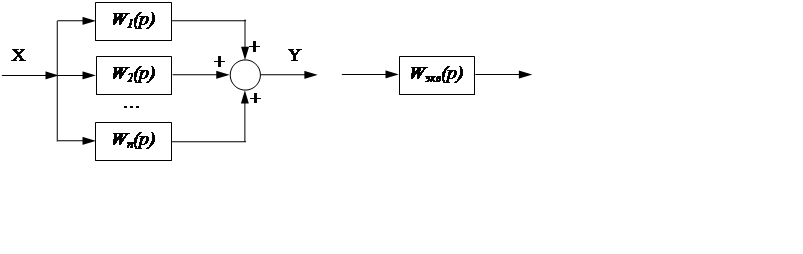
Рисунок 13.  Параллельное соединение звеньев

1.  Звено, охваченное обратной связью (рисунок 14), можно заменить одним звеном с передаточной функцией:

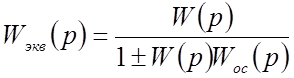,                                    (71)

где “+” – соответствует отрицательной обратной связи;

“-“ – положительная обратная связь.

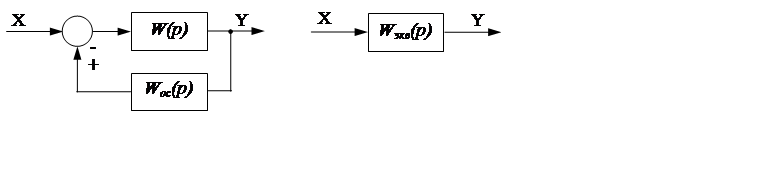
Рисунок 14. Звено, охваченное обратной связью

4. При переносе точки разветвления сигнала через звено по направлению его прохождения (рисунок 15) необходимо в линию связи ответвления включить звено с обратной передаточной функцией звена, через которое осуществляется перенос.

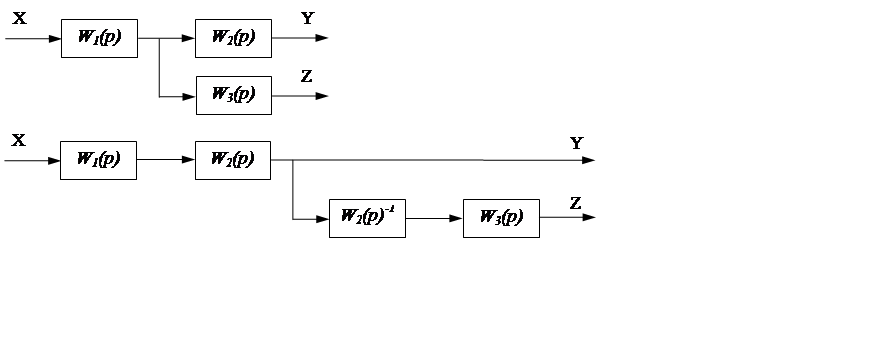
Рисунок 15.  Перенос точки присоединения звена по направлению прохождения сигнала

5. При переносе точки присоединения звена через звено против направления прохождения сигнала (рисунок 16) необходимо в линию связи ответвления включить звено с передаточной функцией звена, через которое осуществлялся перенос.

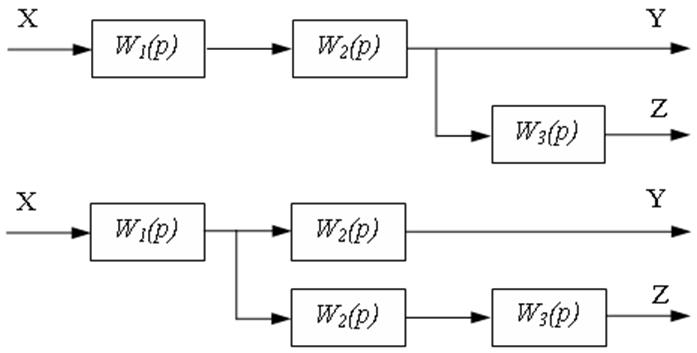
Рисунок 16. Перенос точки присоединения звена против прохождения сигнала

Другие возможные структурные преобразования приведены в таблице 2.

Практика структурных преобразований показывает, что в первую очередь следует устранить перекрёстные обратные связи (если они имеются) и начинать преобразования с внутренних контуров.

Таблица 2 - Структурные преобразования САУ

№	Структурное преобразование	Исходная структура	Преобразованная структура	Выражение для W(p) или выходного сигнала
1	Переста­новка звеньев
2	Перенос линии связи до звена
3	Перенос линии связи за звено
4	Перемена местами линий связи