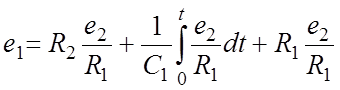 .
(10)
.
(10)
Продифференцируем полученное уравнение:
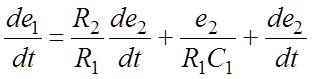 .
(11)
.
(11)
Следовательно, дифференциальное уравнение рассматриваемой цепи имеет вид:
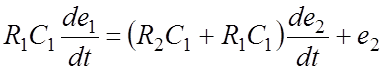 .
(12)
.
(12)
Обозначив
![]() получим:
получим:
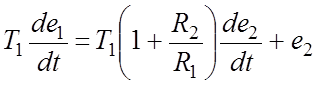 .
(13)
.
(13)
Второй способ.
Для
получения дифференциального уравнения воспользуемся операторной формой записи
сопротивлений: индуктивного![]() , емкостного
, емкостного 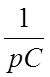 , активного R,
где
, активного R,
где 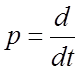 - символ дифференцирования.
- символ дифференцирования.
Преобразуем электрическую цепь рисунка 1 (а) в эквивалентную схему рисунок 1 (б)
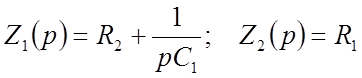 .
(14)
.
(14)
Следовательно:
![]() ;
(15)
;
(15)
![]() .
(16)
.
(16)
Передаточная функция:
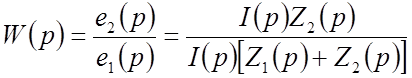 .
(17)
.
(17)
Подставив
значения ![]() и
и ![]() ,
получим:
,
получим:
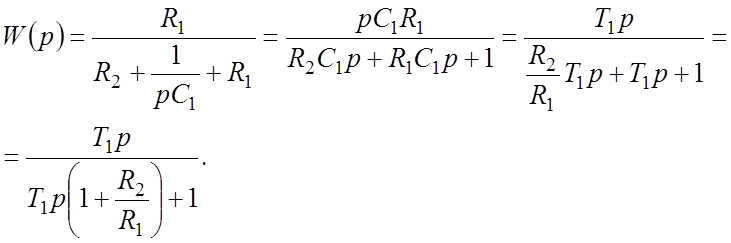 (18)
(18)
Таким образом, по определению передаточной функции
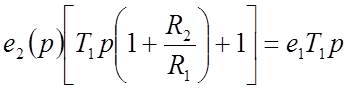 .
(19)
.
(19)
Следовательно:
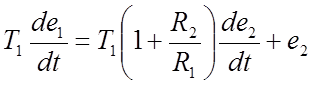 .
(20)
.
(20)
Пример 1.2. Найти дифференциальное уравнение и передаточную функцию мостовой схемы представленной на рисунке 2.
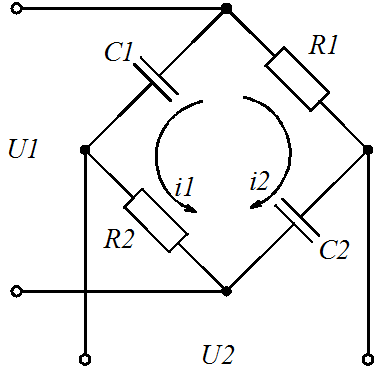 |
Рисунок 2. Пассивная мостовая RC цепь
Решение. Токи плеч моста:
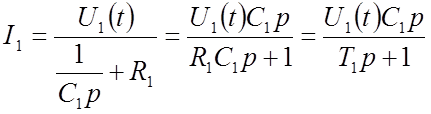 ;
(21)
;
(21)
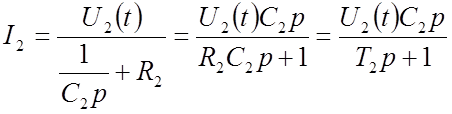 ,
(22)
,
(22)
где
![]() и
и
![]() .
.
Напряжение ![]() определяется:
определяется:
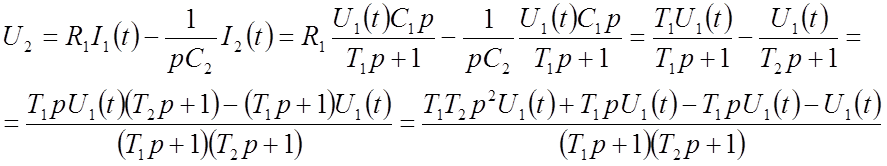 . (23)
. (23)
Следовательно, дифференциальное уравнение имеет вид:
![]() . (24)
. (24)
Передаточная функция определяется:
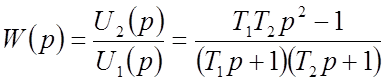 . (25)
. (25)
Пример 1.3. Определить дифференциальное
уравнение двигателя постоянного тока с независимым возбуждением при управлении
изменением напряжения на якоре. Принять: ![]() ,
, ![]() ,
, ![]() .
.
Решение. Основное уравнение движения электропривода (второй закон Ньютона):
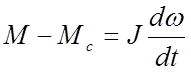 .
(26)
.
(26)
Поскольку ![]() , то
, то 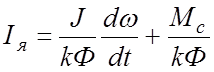 .
.
Уравнение электрического равновесия для цепи якоря (второй закон Кирхгофа):
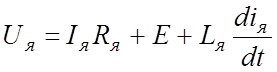 , где
, где ![]() ; (27)
; (27)
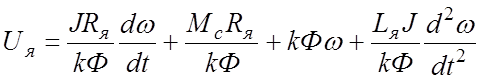 .
(28)
.
(28)
Поделив правую и левую
части уравнения на ![]() и умножив и разделив коэффициент
при
и умножив и разделив коэффициент
при 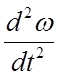 на
на ![]() получим:
получим:
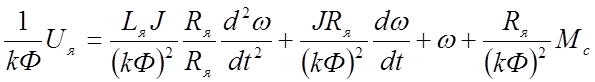 . (29)
. (29)
Обозначим:
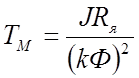 -
электромеханическая постоянная времени;
-
электромеханическая постоянная времени;
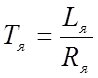 -
электромагнитная постоянная времени;
-
электромагнитная постоянная времени;
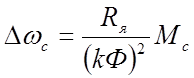 -
«просадка» скорости;
-
«просадка» скорости;
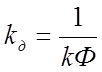 -
коэффициент передачи двигателя по напряжению
-
коэффициент передачи двигателя по напряжению![]() .
.
С учетом принятых обозначений, получим:
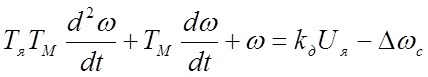 . (30)
. (30)
Пример 1.4. Найти дифференциальное уравнение и передаточную функцию корректирующего устройства постоянного тока с операционным усилителем представленного на рисунке 3.
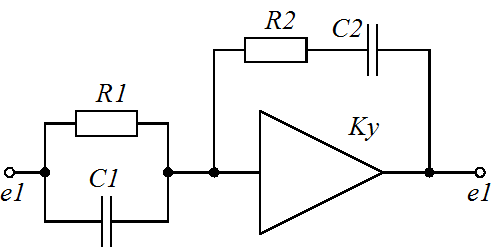
Рисунок 3. Активное корректирующее устройство
![]() Решение. Передаточная функция корректирующего звена при
Решение. Передаточная функция корректирующего звена при ![]() определяется:
определяется:
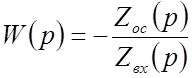 ,
(31)
,
(31)
где 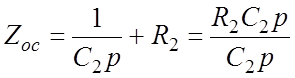 ,
,
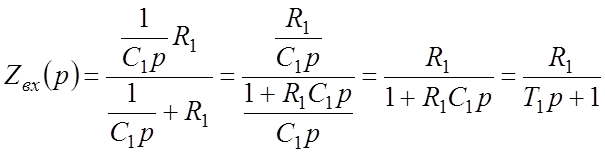 ,
,
![]() ,
, ![]() ,
, ![]() .
.
Следовательно, передаточная функция:
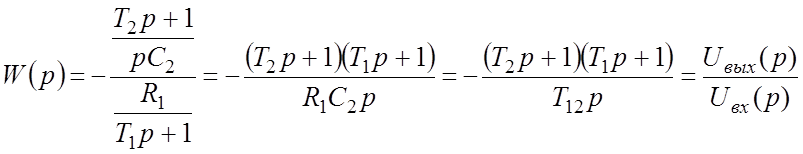 . (32)
. (32)
Дифференциальное уравнение:
![]() , (33)
, (33)
или
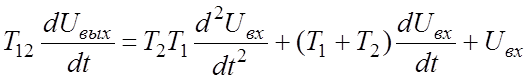 . (34)
. (34)
1.1 Задание к разделу 1
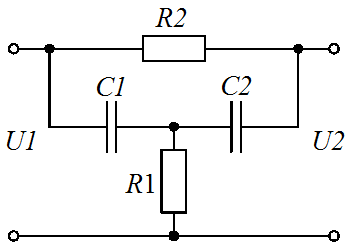
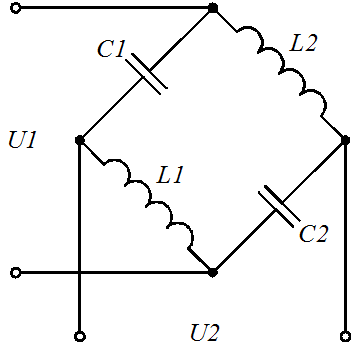
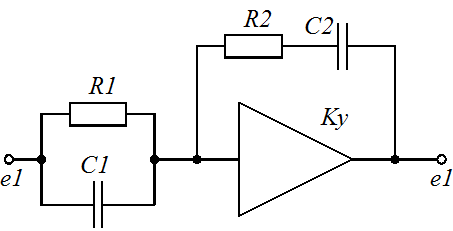
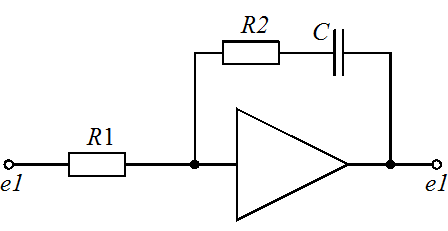
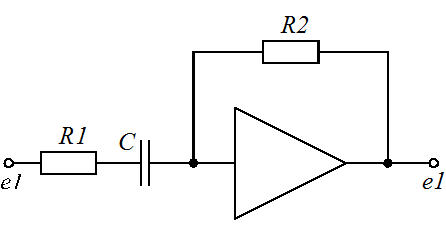
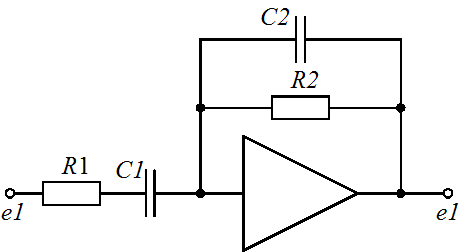
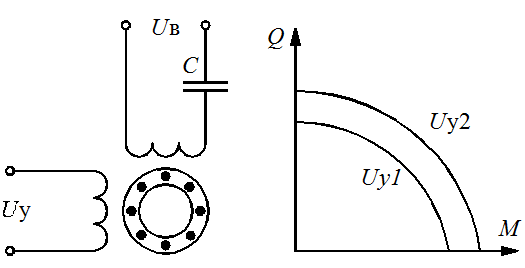
Задание 1.1. Найти дифференциальные уравнения и передаточные функции для представленных на рисунке 4(а-к) схемах.
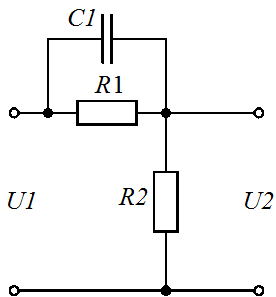
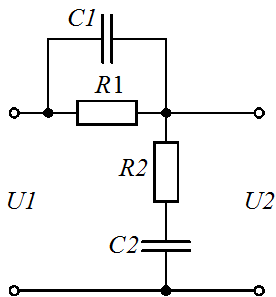
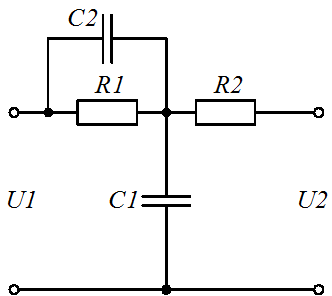
а) б) в)
г) д)
е) ж)
з) и)
 к)
к)
Рисунок 4. Схемы для выполнения задания
Математическое описание динамики САУ обычно производится путем составления системы дифференциальных уравнений. В общем случае любая реальная динамическая система является нелинейной. Однако большинство непрерывных систем управления могут быть линеаризованы, т.е. заменены приближенно эквивалентными системами, переходные процессы в которых описываются обыкновенными дифференциальными уравнениями с постоянными коэффициентами.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.