При составлении дифференциальных уравнений САУ основной задачей является получение дифференциальных уравнений отдельных звеньев системы. Для математического описания САУ её разбивают на динамические звенья. Под динамическим звеном понимают часть системы, которая описывается дифференциальным или иным уравнением определённого вида. В качестве динамических звеньев могут рассматриваться конструктивно обособленные части САУ, например, обмотки возбуждения генераторов, якорные обмотки двигателей, отдельные каскады усилителей и т.д. Иногда динамические звенья могут вообще не иметь физического смысла, характеризуя лишь математическую зависимость между некоторыми величинами САУ.
При составлении уравнений звена следует:
§ определить входную и выходную величину звена и установить дополнительные факторы, от которых зависит выходная величина;
§ выбрать начало отсчета и положительное направление отсчета всех входящих в рассмотрение переменных;
§ ввести соответствующие упрощения, допущения;
§ используя физические законы той отрасли науки и техники, к которой относится исследуемое звено, составить уравнение. Для получения уравнений электрических звеньев используются законы Кирхгофа, для механических звеньев – закон Ньютона, для гидравлических и пневматических звеньев – законы сохранения энергии и вещества, для тепловых устройств – уравнения энергетического баланса и т.д.
В теории автоматического управления принято записывать дифференциальные уравнения в двух стандартных формах:
«Классическая» форма записи:
1. Выходная величина Y и все её производные переносятся в левую часть уравнения, входная величина X, её производные и возмущающее воздействие f – в правую;
2. Коэффициент при выходной величине Y должен быть равен единице;
3. Постоянные времени Тi записываются в степени соответствующей производной.
Рассмотрим пример первой формы записи:
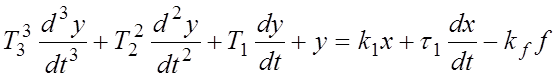 .
(1)
.
(1)
Здесь
Т1, Т2, Т3, ![]() - постоянные
времени,
- постоянные
времени, ![]() ,
, ![]() - коэффициенты,
t – текущее время.
- коэффициенты,
t – текущее время.
Обозначив
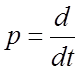 - символ дифференцирования, получим более
компактную форму записи:
- символ дифференцирования, получим более
компактную форму записи:
![]() .
(2)
.
(2)
«Операторная» форма записи:
Считая
условно 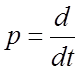 алгебраической величиной, решим
уравнение (2) относительно выходной переменной
алгебраической величиной, решим
уравнение (2) относительно выходной переменной
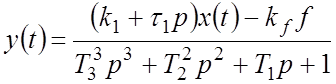 .
(3)
.
(3)
Передаточной
функцией звена по определённому внешнему воздействию называется отношение
изображения по Лапласу выходной величины ![]() к
изображению по Лапласу рассматриваемого воздействия
к
изображению по Лапласу рассматриваемого воздействия ![]() (i–
номер входного воздействия) при нулевых начальных условиях и других внешних
воздействиях равных нулю:
(i–
номер входного воздействия) при нулевых начальных условиях и других внешних
воздействиях равных нулю:
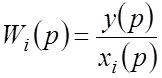 .
(4)
.
(4)
Для получения передаточной функции следует:
§ записать
уравнение звена в символической форме, заменив 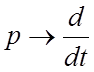 ;
;
§ формально разделить символический многочлен, стоящий множителем в правой части уравнения перед рассматриваемым внешним воздействием, на символический многочлен в левой части уравнения, являющийся множителем перед выходной координатой:
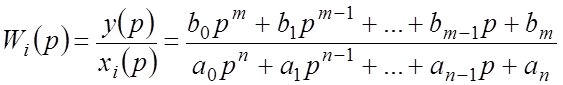 .
(5)
.
(5)
Поскольку
конкретный вид управляющих воздействий ![]() и
возмущающих воздействий
и
возмущающих воздействий ![]() не оговариваются, то
передаточная функция звена не зависит от закона изменения воздействий и
определяется только свойствами самого звена.
не оговариваются, то
передаточная функция звена не зависит от закона изменения воздействий и
определяется только свойствами самого звена.
Для получения дифференциального уравнения звена по передаточной функции следует записать операторное уравнение звена:
![]() ,(6)
,(6)
и
заменить оператор Лапласа 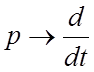 :
:
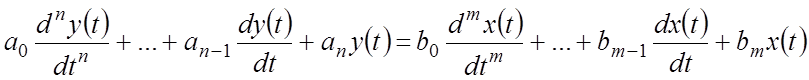 .
(7)
.
(7)
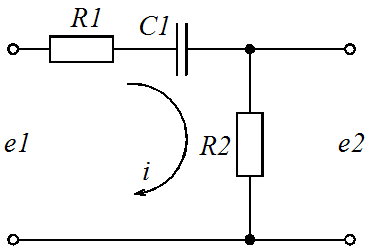
Пример 1.1. Вывести дифференциальное уравнение пассивного электрического корректирующего устройства постоянного тока представленного на рисунке 1.
 |
 |
(а) (б)
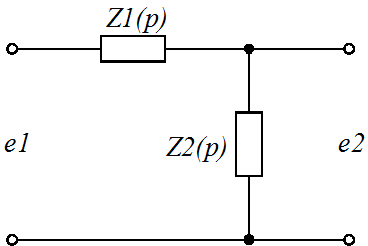
Рисунок 1. Пассивное корректирующее устройство (а) и эквивалентная схема (б)
Решение:
Первый способ.
Используя закон Кирхгофа, можно записать два уравнения:
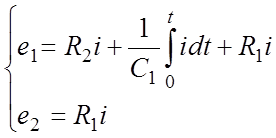 .
(8)
.
(8)
Из
второго уравнения:![]()
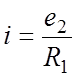 .
(9)
.
(9)
Подставим выражение для тока в первое уравнение:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.