Дифференциальные уравнения и передаточные функции звеньев САУ. Линеаризация нелинейных статических характеристик и нелинейных уравнений. Составление и преобразование структурных схем САУ. ТАУ. Часть 1: Методические материалы и указания к практическим занятиям, страница 4

Линеаризацией называется замена реальных нелинейных уравнений близкими к ним линейными уравнениями. Линеаризация исходных нелинейных зависимостей основана на методе малых отклонений, сущность которого заключена в том, что динамические свойства звеньев и систем исследуется не во всем диапазоне изменения переменных, а вблизи их некоторых значений, соответствующих характерным режимам работы (например: установившемся режимам). Основой линеаризации является выдвинутое И.А. Вышнеградским предположение, что в течение всего процесса регулирования имеют место лишь достаточно малые отклонения всех измеряющихся параметров от их установившихся значений.

Линеаризация возможна, если:

§  отклонение переменных малы;

§  линеаризуемая функция аналитична, т.е. имеет конечные производные всех порядков в окрестности точки линеаризации.

Пусть задано нелинейное дифференциальное уравнение звена САУ:                                 .                                             (35)

Уравнение для установившегося режима :

.                                             (36)

Исходное нелинейное уравнение в отклонениях имеет вид:

.                                 (37)

Разложив левую часть уравнения в ряд Тейлора в окрестности точки установившегося режима , получим:

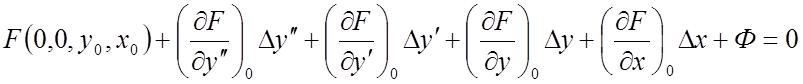,  (38)

где 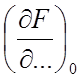 - частные производные в точки установившегося режима;

 - члены высшего порядка малости, состоящий из произведения отклонений, степеней отклонений  с коэффициентами в виде смешанных частных производных и производных второго и высших порядков от F по соответствующим аргументам.

Отбросив нелинейный остаток , получим линейное дифференциальное уравнение с постоянными коэффициентами, которые являются результатом линеаризации исходного дифференциального уравнения.

При стандартной форме записи уравнений в ТАУ принято оставлять в левой части выходную величину и её производные, входная величина, её производные и другие величины (возмущения) переносятся в правую часть уравнения:

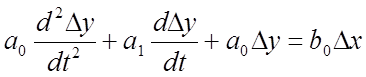,                          (39)

где .

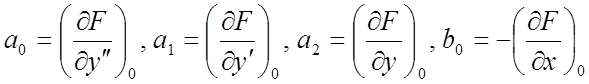Погрешность линеаризации оценивается величиной относительной погрешности:

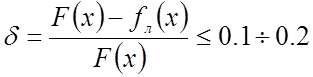,                            (40)

где  - исходная нелинейная функция;

 - уравнение линеаризованной характеристики.

Заметим, что линеаризация методом касательной (разложением в ряд Тейлора) дает хорошее совпадение вблизи точки установившегося режима и худшее у границ рабочей зоны. Линеаризация по методу секущей (метод осреднения) дает хорошее совпадение «в среднем», хотя наклон секущей не совпадает с наклоном кривой в рабочей точке представленной на рисунке 5.

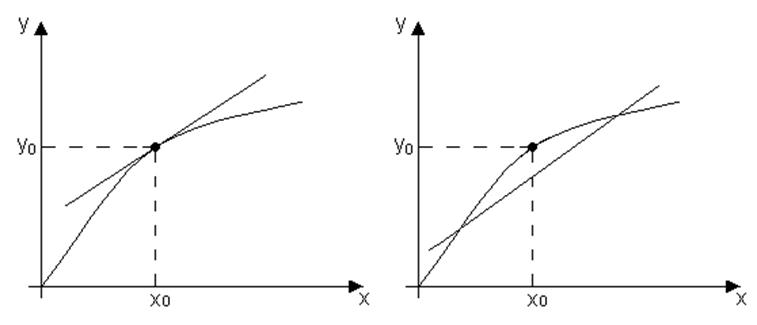                                 а)                                                     б)

Рисунок 5. Линеаризация нелинейной характеристики методом касательной (а) и методом секущей (б)

Пример 2.1. В окрестности точки установившегося режима аналитически линеаризовать нелинейное уравнение .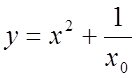

Решение. Разложим уравнение  в ряд Тейлора в окрестности точки установившегося режима:

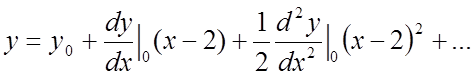 ,                       (41)

где .

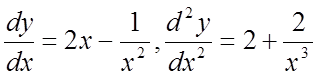В точке установившегося режима:

;

;

.

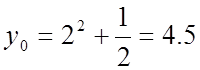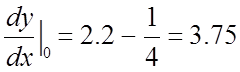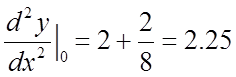Таким образом:

.                 (42)

Ограничившись линейными членами разложения получим:

.                        (43)

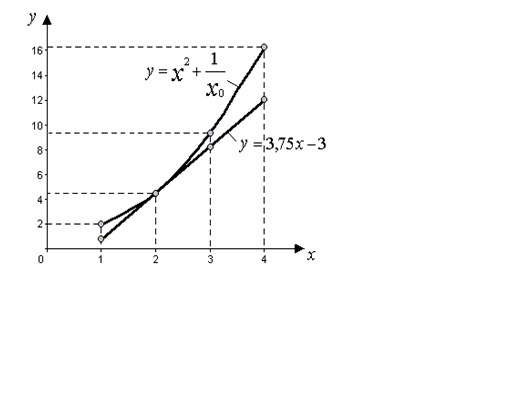
На рисунке 6. приведена линеаризация рассматриваемой нелинейной функции.

X	1	2	3	4
Y	2	4.5	9.3	16.25

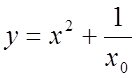
X	1	2	3	4
Y	0.75	4.5	8.25	12

                                                                                                                

Рисунок 6. Линеаризация нелинейного уравнения методом касательной

Пример 2.2. Вывести дифференциальное уравнение движения асинхронного двигателя с короткозамкнутым ротором представленного на рисунке 7.

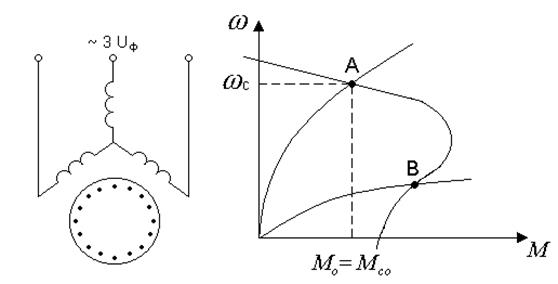Рисунок 7. Схема включения и механическая характеристика АД с короткозамкнутым ротором

Рабочий механизм с вентиляторной характеристикой: