Лекции по дисциплине "Антенно-фидерные устройства СВЧ диапазона", страница 9

Обозначим d шаг между излучателями (период решётки). Рассмотрим поле излучения решётки в некотором произвольном направлении θ (угол будем отсчитывать относительно нормали к решётке), расстояние от края решётки до точки наблюдения обозначим r.

Выберем это расстояние большим, >> размеров решётки, r >> L = d*N, чтобы все лучи, идущие в точку наблюдения от каждого излучателя, можно было считать параллельными.

В силу принципа суперпозиции, суммарное поле антенны равно сумме полей излучения отдельных её элементов. Пусть поле первого излучателя в точке наблюдения равно Е₁.Так как мы договорились, что все излучатели решётки возбуждаются с одинаковой амплитудой I, а Е ~ I exp(-jkr) [здесь мы не можем опустить экспоненту, так как расстояния от всех излучателей до точки наблюдения различны], то

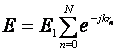, где А – постоянный множитель, одинаковый для всех n.

Очевидно, что r_n = r + d*n*sinθ, следовательно,

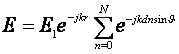
Нетрудно заметить, что наша сумма – это сума членов геометрической прогрессии  со знаменателем q = exp(-jkdsinθ) .

Как вы, я надеюсь, помните, 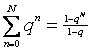. Следовательно,

Выполним стандартное преобразование этого выражения, вынеся за скобку экспоненту половинного аргумента: exp(1/2 kdNsinθ) в числителе и exp(1/2 kdsinθ) – в знаменателе.

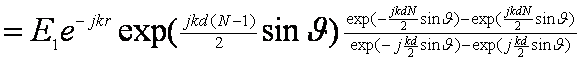
Выражения, стоящие в числителе и знаменателе, - это синусы своих аргументов (с точностью до деления на 2j), следовательно,

,

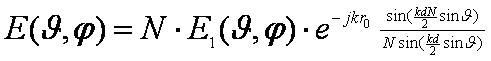где r₀ – расстояние от центра решётки до точки наблюдения.

Параметр u = kd/2 sinθ  называется обобщённой угловой координатой, и в этих обозначениях диаграмму направленности нашей решётки в плоскости θ можно записать в следующем виде:

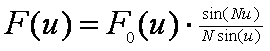
В этом выражении можно выделить два сомножителя: первый – это диаграмма направленности одиночного излучателя, второй множитель учитывает расположение излучателей в решётке и называется множителем решётки.

Это – так называемая теорема о перемножении диаграмм направленности.

Рассмотрим более подробно множитель решётки.

Очевидно, при малых значениях угла θ, т.е. вблизи нормали к решётке, аргументы синусов в числителе и знаменателе малы, и нетрудно видеть, что предел этого выражения при θ → 0 равен единице.

При аргументе синуса в числителе, кратном π,  Nu = mπ числитель обращается в нуль, в знаменателе при этом имеем sin(mπ/N) ≠ 0 для всех m = 1, …, N-1. Это – нули множителя ДН:

kdN/2 sinθ₀ = mπ, . sinθ₀ = 2mπ/ kdN = mλ/dN.

Первый нуль соответствует m = 1. Для больших решёток, N » 1, sinθ₀¹ ≈ θ₀¹ = λ/dN. Это – половина ширины главного лепестка ДН «по нулям».

Отсюда следует, что главный лепесток тем уже, чем длиннее наша линейная решётка в длинах волн.

Пусть, например, в решётке 20 элементов с шагом d = λ/2, т.е. Длина решётки равна 10λ. Тогда θ₀¹ = λ/10λ = 0.1 ≈ 5,7.

Определим теперь направления боковых лепестков. Приближённо это те направления, в которых числитель максимален (=1) (на самом деле максимумы немного смещены влево из-за множителя 1/N), т.е. аргумент синуса

kdN/2 sinθ_max = (2m+1)π/2,

откуда sinθ_max = (2m+1)π/2 /(πdN/λ) = (2m+1) λ/(2dN). Здесь m = 1,2,…

Оценим уровни этих боковых лепестков по отношению  к главному максимуму ДН (=1!).

Они равны, очевидно, 1/(N sin(kd/2 sinθ_max) = 1/Nsin(kd/2*(2m+1) λ/(2dN)) =

= 1/(Nsin((2m+1)π/(2N)).