Лекции по дисциплине "Антенно-фидерные устройства СВЧ диапазона", страница 12

Наконец, не всегда требуется не допустить дифракционный максимум вообще ни при каких углах. Дело в том, что сканирование главного луча происходит в пределах парциальной ДН излучателя, которая, естественно, не перемещается при сканировании ДН решётки (на графике– пунктиром, взята ДН в форме cos²θ, $ только в зоне видимости):

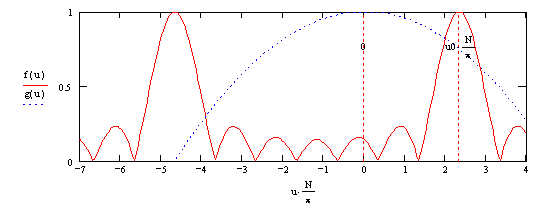
На графике изображена ДН решётки из N = 7 излучателей с периодом d = 0.67 λ, отсканированная на 30°.

Как видим, при этом максимум дифракционного лепестка находится точно на границе зоны видимости, как мы и потребовали, выбирая d. При расчёте ДН решётки его ещё нужно будет умножить на парциальную ДН (по теореме перемножения ДН), в результате чего его реальный уровень будет ниже:

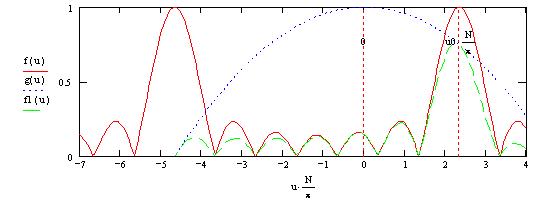
Поэтому можно допустить его приближение к нормали до некоторого угла θ₂ < 90°, до тех пор, пока это не приведёт к чрезмерному возрастанию боковых лепестков.

Потребуем, чтобы kd/2 sinθ₂ - kd/2·sinθ₁ = π, откуда

d = λ/(sinθ₂ + sinθ₁).

Возьмём, например, θ₂ = 70°. Тогда получаем d = 0.695, и наша ДН имеет вид:

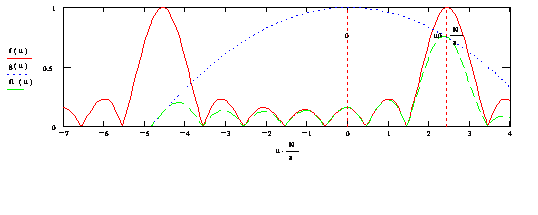
Т.е. такое увеличение d не привело к возрастанию уровня боковых лепестков.

В результате мы при построении решётки можем сэкономить 1 – (0.5/0.695) = 28% излучателей. Если решётка большая, содержит порядка сотни излучателей, эта экономия выразится солидной суммой.

Всегда при проектировании антенны ищут самый простой и экономичный вариант. Это особенно важно, когда разрабатывается ФАР, содержащая в своём составе аппаратуру управления, стоимость которой прямо пропорциональна количеству управляемых каналов антенны.

Лекция 11 (20.10.05)

Рассмотренный на прошлой лекции способ управления положением максимума ДН в пространстве (с помощью фазовращателей) называется фазовым сканированием.

Существует ещё один способ электрического сканирования, не требующий применения специальных устройств. Это метод частотного сканирования ДН. Он заключается в следующем.

Пусть излучатели линейной решётки запитываются последовательно от некоторой магистральной линии:

Сигнал, проходя от источника по этой линии расстояние x, испытывает задержку по фазе, равную βx, где β – постоянная распространения волны в этой линии. В общем случае в линии β ≠ k, например, как вы знаете в прямоугольном волноводе

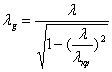, и 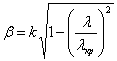, где λ_кр – критическая длина волны, равная для прямоугольного  волновода ….?  2a (удвоенному размеру широкой стенки). Для других волноводов, как вы знаете, эта формула также справедлива, но критическая длина волны там определяется по-другому.

Очевидно, что  β < k, т. е. в канализирующей линии имеет место замедление волны (вспомним, что v_гр  =   β/ω).

А может быть β = k?  (В односвязных волноводах!)

Путь l, проходимый волной по канализирующей линии от одного излучателя до другого, не обязательно равен   периоду решётки d (т.е. расстоянию между излучателями). Он может быть больше (и так и делают  специально) за счёт введения в магистральную линию задержек:

( Рисунок)

Тогда сдвиг фазы по питанию между соседними излучателями запишем как   βl, и фаза  ψ_n тока возбуждения n-го излучателя запишется как  nβl.

Вспомним выражение для ДН  равноамплитудной решётки: 

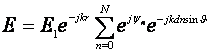
  Рассуждая так же, как и раньше,  мы можем сказать, что максимум θ₀ этой ДН определяется из условия:

ψ_n = k d n sin(θ₀), или βl =  kd  sin(θ₀).

Перепишем последнее условие, выразив β и k через частоты.  Так как