Лекции по дисциплине "Антенно-фидерные устройства СВЧ диапазона", страница 6

Где С = 0,557 – постоянная Эйлера.

Современные вычислительные средства позволяют вычислить интеграл непосредственно и построить график:

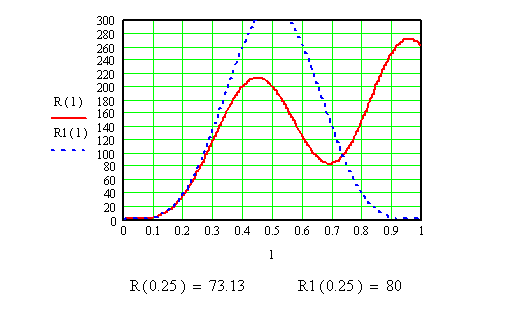
Здесь синяя (штриховая) кривая – приближённое решение, красная – уточнённое. Спадающие участки на ней вызваны появлением противофазных участков, приводящим к снижению излучаемой мощности, следовательно – к уменьшению сопротивления излучения.

Как уже отмечалось понятие сопротивления излучения тесно связано с другой энергетической характеристикой антенны – коэффициентом направленного действия D. Действительно, D = П_макс/П_ср = Е_макс²/(2Z_c) 4πr²/P = Е_макс² r²/(30 I_max² R_{изл п}), так как

(Е_максr)² = {60I_max [1 - cos(kl)]}²

P = I_max² R_{изл п}/2, следовательно,

D = {60I_max [1 - cos(kl)]}² 4π / (I_max² R_{изл п}/2) = 480 sin⁴(kl/2)/R_{изл п} =

= 8 sin⁴(kl/2)/ ∫[cos(klcosθ) - cos(kl)]²/sinθ dθ

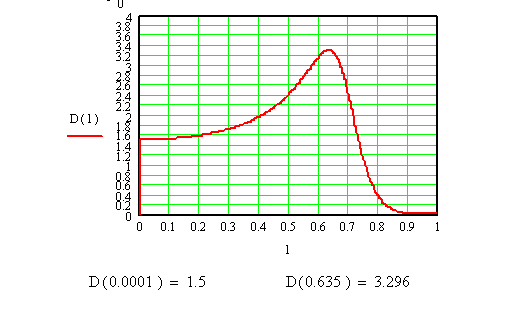
Проанализируем полученную формулу для нескольких конкретных случаев.

1. ДипольГерца.

Для него Е_макс r/ I_max = 30kl, R_изл = 20 k²l², тогда D = (Е_макс r/ I_max)²/30R_изл = 1,5 – известный результат!

2. Полуволновый вибратор. l = λ/4→ kl = π/2, Е_макс r/ I_max = 60(1-cos kl) = 60, и мы знаем R_изл = 73,1. Находим:

D = 60²/(30 73,1) = 1,64

КНД имеет максимум при l = 0,635λ, равный 3,3. (Этому случаю соответствует ширина ДН = 31˚).

При дальнейшем увеличении длины КНД падает в связи с появлением всё возрастающих боковых лепестков. При l = λ главный максимум исчезает полностью, чему соответствует D = 0.

На практике часто определяют КНД по отношению к полуволновому вибратору, для которого D = 1,64. (Т.е. он занижен по отношению к изотропному излучателю в 1,64 раза).

Симметричный вибратор над металлическим экраном

1.  Точечный электрический заряд над металлическим экраном.

(Метод зеркальных изображений, Белоцерковский)

2.  Вибратор параллелен металлическому экрану.

-  Противофазность

-  Разность хода.

ДН в поперечной плоскости. Интерференционный множитель – sin(khsinα). Собственная ДН – ненаправленная.

Максимумы ДН: khsinα_n = (2n+1)π/2,  sinα_max = (2n+1)λ/(4h)

Нули: khsinα_n = nπ, sinα₀ = nλ/(2h)

h = 0.25λ  4h/λ = 1 Max: единственное решение – n = 0, -> sin = 1,   α_max = 90˚

Нули: sinα₀ = 2n, единственное решение – n = 0, -> sin = 0,   α₀ = 0˚.

h = 0.25λ                                                     

  

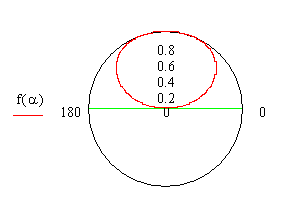
h = 0.5λ.

sinα_max = n+1/2, единственное решение – n = 0, -> sin = 1/2,   α_max = 30˚

sinα₀ = n, n = 0 или 1 – два нуля:  0˚и 90˚

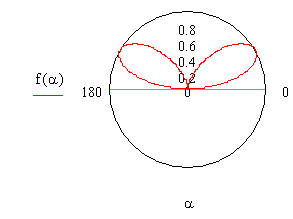
Промежуточный случай: h = 0,4λ.

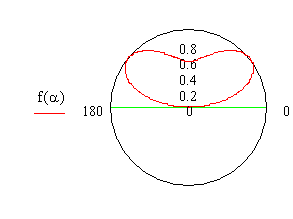
h = λ.

sinα_max = (2n+1)/4, два решения – n = 0, -> sin = 1/4,   α_max = 20˚ и n = 1, α_max ≈ 48˚

sinα₀ = n/2, n = 0, 1 или 2 – три нуля:  0˚, 30˚и 90˚.