Лекции по дисциплине "Антенно-фидерные устройства СВЧ диапазона", страница 14

Мы рассмотрели решётку с равномерным амплитудным распределением. Её ДН имеет довольно высокий уровень боковых лепестков, -13,6 дБ.

На практике часто требуется получить более низкий УБЛ, например, для радиолокационных антенн. Наличие в них боковых лепестков может привести к появлению ложной отметки в направлении бокового лепестка от крупноразмерной цели или помехи.

Для этого применяют спадающие к краям апертуры амплитудные распределения.

Рассмотрим, что произойдёт, если мы выберем косинусное амплитудное распределение, так чтобы максимум был в центре, и на длине решётки укладывался целый период:

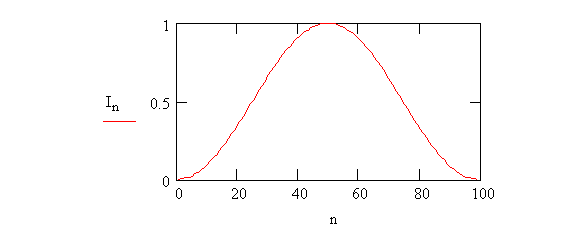
Это можно записать так: I_n = [1 - соs(2πn/N)]/2, n = 0,…,N.

Рассчитаем ДН синфазной решётки с таким амплитудным распределением:

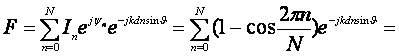
Представим cos в скобках как сумму экспонент, тогда

Первое слагаемое в этой сумме – знакомая вам ДН синфазной решётки с равномерным амплитудным распределением.

Второе и третье слагаемые – ДН этой же решётки с линейным фазовым распределением. Множитель ½ показывает, что максимумы их ДН вдвое меньше первой.  Посмотрим, под какими углами от нормали находятся эти максимумы. Для первой из них:

kdnsin(θ₁) = 2πn/N, 2u₁ = 2π/N, u₁ = π/N.

Как вы помните, это первый нуль ДН, стоящей на нормали.

Аналогично для второго слагаемого  u₂ = - π/N

- это положение нуля с другой стороны от нормали.

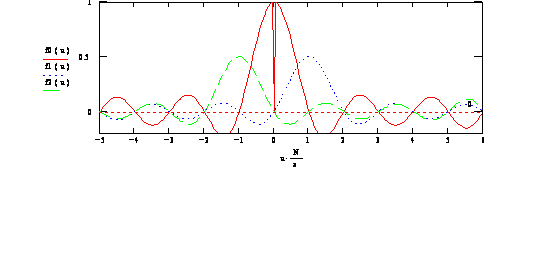
Как вы видите, из-за сдвига на один шаг многие боковые лепестки стали противофазными, в результате чего при суммировании получается следующая ДН:

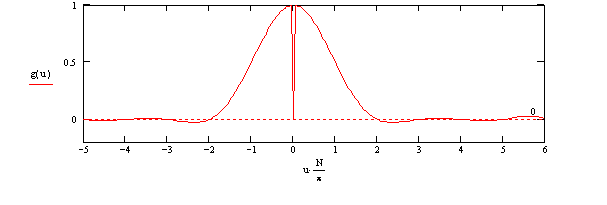
с довольно низкими боковыми лепестками. Как я уже говорил, такие ДН удобнее рассматривать в логарифмическом масштабе:

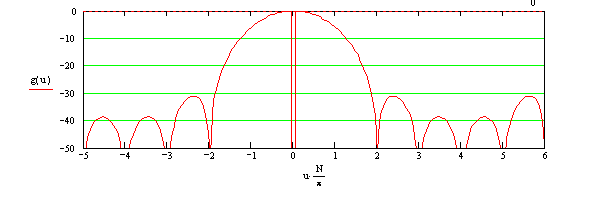
Так как мы рассматривали решётку из M = N + 1 = 9 излучателей, получилась широкая ДН с небольшим количеством боковых лепестков в периоде ДН (зона видимости: ±4).

Для анализа амплитудных распределений часто рассматривают решётки как антенны с непрерывным распределением тока, т.е. как бы с бесконечно малым периодом. При этом суммирование в формуле для ДН заменяется интегрированием, упрощает вычисления и позволяет получить ДН антенны в явном виде. Оказывается, что такое приближение довольно точно описывает ДН дискретной решётки с периодом до λ/2.

Посмотрим, что будет происходить с ДН равноамплитудной антенны при d→0.

sin(0.5kdNsinθ)/(Nsin(0.5kdsinθ)) = sin(0.5kLsinθ)/(Nsin(0.5kdsinθ))→ sin(0.5kLsinθ)/(0.5kLsinθ)) = sinU/U,

где U = kL/2 sinθ – также иногда называют обобщённой угловой координатой, не путать с u = U/N!

В координатах U зона видимости(соотаетствующая углам θ от -90 до +90 градусов) располагается – от - kL/2 до kL/2 и имеет, следовательно, размер = kL.

Эта функция непериодическая: sinU вписывается в огибающую 1/U, F(0)=1.

Рассчитаем теперь ДН с непрерывным амплитудным распределением I(x) = a-bcos(2πx/L), которое можно также записать в общем виде следующим образом, используя формулу для косинуса двойного аргумента. (a –b(2-sin²) = (a-2b) + b sin²), или

, где t = a-b (остался один параметр!).

Это распределение носит имя «косинус квадрат на пьедестале» (пьедестал – t). «Косинус» – потому что обычно отсчитывают координату  х от центра.

Варьируя параметр t, (или a, b), можно, очевидно, изменить соотношение амплитуд трёх составляющих ДН, которую мы рассмотрели выше, и повлиять таким образом на УБЛ.