Лекции по дисциплине "Антенно-фидерные устройства СВЧ диапазона", страница 10

Первый боковой лепесток (m = 1) имеет уровень 1/(Nsin(3π/(2N)) ≈ 2/(3π) ≈ 0.21, т.е примерно 21%, или -13 дБ.

Второй боковой лепесток (m = 2) имеет уровень 1/(Nsin(5π/(2N)) ≈ 2/(5π) ≈ 0.13 и т.д..

Как мы видим, уровни боковых лепестков не зависят от количества элементов решётки N и периода решётки d.

Количество боковых лепестков решётки (нули: m = 1…N) тем больше, чем больше количество излучателей решётки. Естественно, что они при этом сужаются.

Ширина главного лепестка ДН также тем меньше, чем длиннее решётка. Мы определили её по нулевому уровню как 2λ/dN = 2λ/L. Расчёт показывает, что ширина это ДН по уровню половинной мощности ∆θ_0,7 примерно равна половинной ширине по нулевому уровню:

 ∆θ_0,7 ≈ 1/(L/λ), или в градусах (умножаем на 180°/ π ≈ 57°) = 51°/(L/λ).

21.10.03

Проанализируем множитель решётки

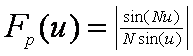
в обобщённых угловых координатах (u). Формально, забыв, что u = kd/2 sin(θ) и  не может быть больше  kd/2 по модулю, можно рассматривать в качестве области определения этой функции всю числовую ось, от - ∞ до + ∞. Очевидно, что эта функция периодична с периодом π, так как N – целое число (количество излучателей в нашей решётке). При u = 0, π, 2π, 3π, … числитель и знаменатель обращаются в нуль. Раскрывая эту неопределённость, получаем в этих точках F_р = 1, т.е. такие же максимумы, как на нормали, при u = 0. При изменении u от 0 до π/2 боковые лепестки спадают, затем симметрично относительно этой точки возрастают в обратном порядке. Изобразим это на графике, отложив по оси абсцисс Nu/π для N = 7:

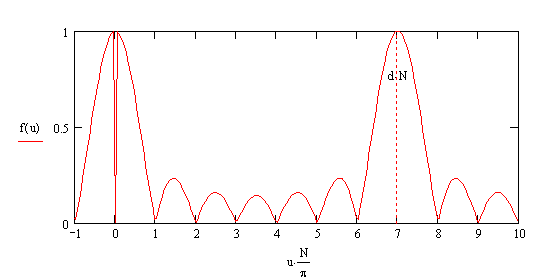
На оси u, как вы помните, только небольшая часть значений соответствует реальным углам θ: это [-kd/2, kd/2]. На нашем графике это kd/2 *N/π = dN/λ = L/λ, где L – длина нашей решётки. Найдём условие, при котором вторичный максимум не появится в области реальных углов, в зоне видимости. Для этого должно быть, очевидно, θ < 90°, u_max = kd/2 < π. Т.е. d/λ < 1, d < λ. На графике это соответствует точке Nu/π = Nπ/π = N. Таким образом, для того чтобы вторичный, или дифракционный, максимум не появлялся в области реальных углов, необходимо, чтобы период решётки был меньше длины волны (на картинке d = λ).

То, что при d = λ поля излучения элементов решётки складываются синфазно, помимо нормали к решётке, вдоль её оси, вполне очевидно: поле излучения, пройдя путь от одного излучателя до соседнего с ним (длиной d = λ), испытывает сдвиг по фазе = kd = 2π d/λ = 2π, т.е. оказывается синфазным с излучением своего соседа, и т.д.. Если расстояние d > λ, то, очевидно, существует угол θ^* < 90°, для которого сдвиг по фазе излучений соседних элементов равен 2:

   θ^*

λ

d > λ

, т.е. в некотором направлении θ^* формируется дополнительный максимум излучения. Понятно, что второй такой же максимум образуется при θ = -θ^*.

Выше мы получили это результат формально, рассматривая ДН в обобщённых угловых координатах.

Ещё раз вернёмся к нашей картинке. Подчёркиваю: период функции F_p(u), или расстояние между максимумами ДН на оси u, равен 2π при любых расстояниях между излучателями d и любом их количестве N, в то время как зона видимости определяется межэлементным расстоянием  решётки. Зона видимости может быть как больше, так и меньше периода ДН. Это означает, что в области реальных углов могут существовать дифракционные максимумы, что происходит, если расстояние между элементами решётки больше длины волны.