Аналогові та підсилювальні електронні пристрої. Частина 2: Навчальний посібник, страница 4

Останній рядок таблиці дозволяє будувати логарифмічні частотні характеристики, використовуючи значення  як точки на осі частот, після якої вони одержують нахил – 12 дБ/окт.

Усе розглянуте стосується так званої високочастотної корекції, коли внаслідок її дії смуга пропускання збільшується у бік високих частот. Часто виникає необхідність покращити частотну характеристику у області нижніх частот, тобто розширити смугу пропускання у такий спосіб, щоб пристрій ефективно підсилював низькі частоти.

Корекція, що розширює смугу пропускання в область більш низьких частот чи покращувальна характеристика у цій області, зветься низькочастотною. Частотна характеристика для області нижніх частот

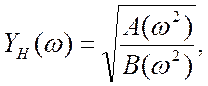
має такі особливості:  отже поліноми  та  повинні мати однакові коефіцієнти при найвищих степенях  і ці степені повинні бути однаковими:  отже, поліном  не повинен містити постійного члена. Тоді

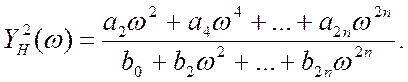
Проведемо інверсію частоти та введемо нову частоту 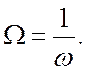 Потім поділивши чисельник та знаменник на  дістанемо

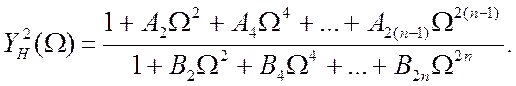
Ця форма запису характеристики тотожна тій, що розглянута вище. Отже, до неї застосовується все те, що раніше було запропоновано до ВЧ корекції. Розширення смуги пропускання, тобто збільшення  у цьому випадку буде в дійсності означати розширення смуги пропускання у бік нижніх частот (зниження 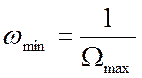). У такий спосіб "інверсією частоти" користуються не тільки при аналізі схем НЧ корекції, але і при їх синтезі.

1.3 Корекція характеристик за допомогою коригувальних індуктивностей

Каскад з індуктивною корекцією показано на рис.1.6 (а).

 

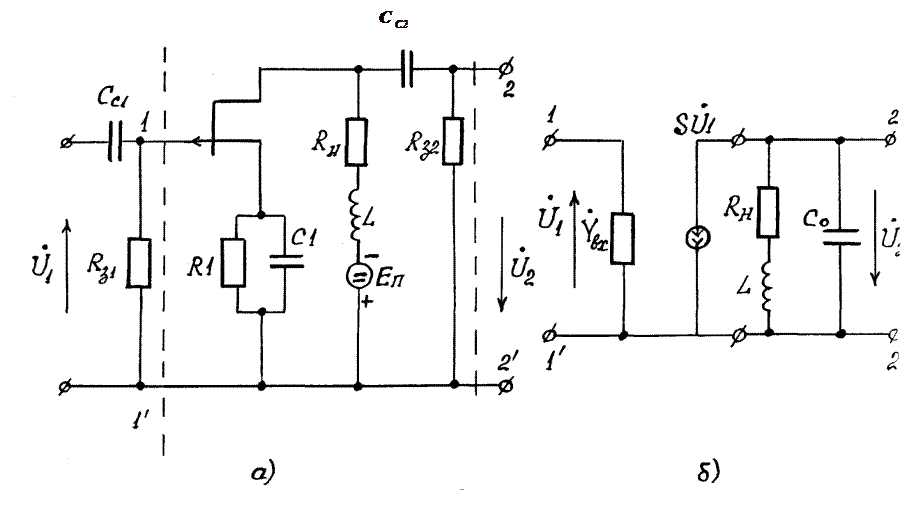Рисунок 1.6 – Паралельно – індуктивна корекція

Корекція здійснюється за допомогою L, що включається послідовно з навантаженням. Така корекція зветься двополюсною або паралельною ВЧ корекцією. Розширення смуги частот у цьому випадку пояснюється тим, що коригуюча індуктивність L, навантаження  та повна ємність каскаду  утворюють резонансний контур. На низьких та середніх частотах навантаження транзистора практично дорівнює  На ВЧ  при відповідному виборі резонансної частоти  та резонансного опору  можна дістати підсилення  тоді як у звичайних каскадах на цих частотах воно вже суттєво менше за

Індуктивність L впливає на властивості каскаду тільки в області верхніх частот, тому розрахункові формули для області НЧ та СЧ лишаються без змін. Еквівалентна схема каскаду для верхніх частот показана на рис.1.6(б). Щоб здобути широку смугу, опір навантаження транзистора вибирається невеликим. Це дозволяє не враховувати в еквівалентній схемі великі опори  та  При цьому підсилення каскаду на середніх частотах

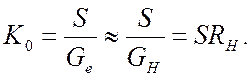
На ВЧ навантаження каскаду являє собою резонансний контур, що має провідність

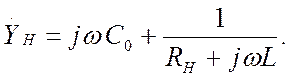
Підсилення на ВЧ відповідно становить

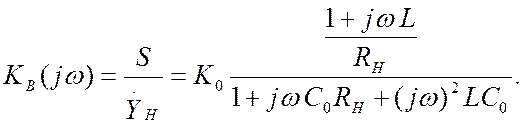
Для спрощення запису позначимо:  – стала часу некоректованого каскаду; 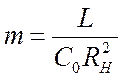 – коефіцієнт корекції, що дорівнює квадрату добротності резонансного контуру.

Тоді

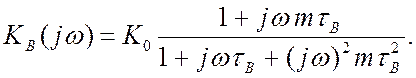
Комплексна частотна характеристика каскаду

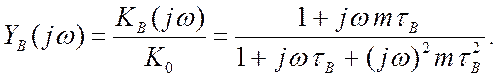
Модуль її дає АЧХ каскаду

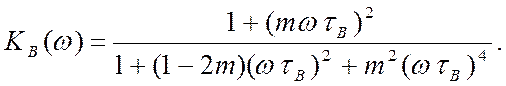                    (1.8)

Аргумент визначає ФЧХ

                          (1.9)

У випадку, коли  та  вирази (1.8) та (1.9) визначають АЧХ та ФЧХ звичайного резисторного каскаду.

Знайдемо коефіцієнт корекції, що забезпечить найбільше розширення смуги без підйому частотної характеристики (оптимальна частотна характеристика).

Згідно з Брауде запишемо  у вигляді відношення двох поліномів зі зростаючими ступенями частоти:

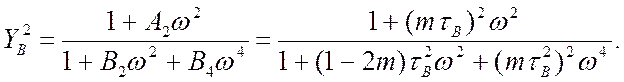
Для корекції необхідно забезпечити  або  звідки

У випадку, коли  на АЧХ виникає підйом, що зростає зі зростанням m. Одночасно з цим має місце незначне зростання смуги частот. На рис.1.7 побудовані АЧХ каскаду для деяких значень m.

Користуючись ними неважко побачити на скільки розширює смугу резисторного каскаду введення корекції, чому дорівнює підйом і т.і. Звичайно, смуга оцінюється на рівні  Тоді для  маємо

 

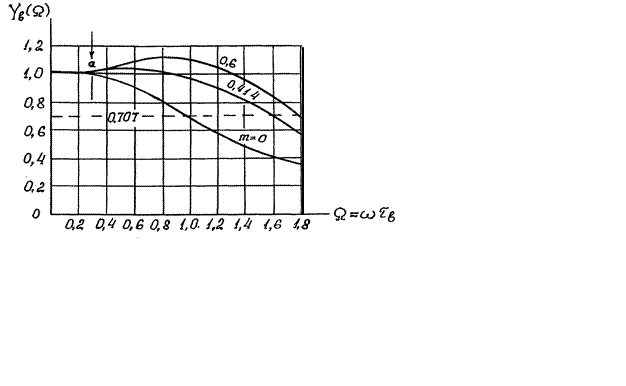Рисунок 1.7 – АЧХ каскаду для значень m

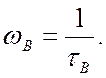 Якщо  гранична частота збільшується до значення  Відношення 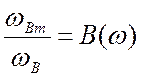 показує у скільки разів розширюється смуга каскаду з корекцією. Залежність  подана на рис.1.8.