Аналогові та підсилювальні електронні пристрої. Частина 2: Навчальний посібник, страница 3

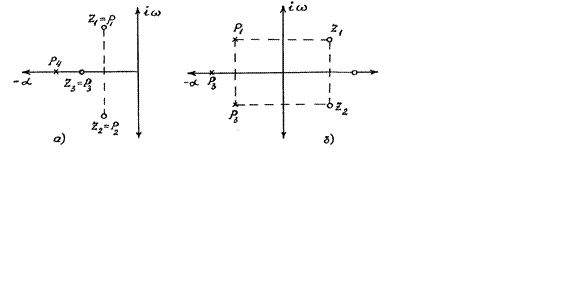
З рис.1.3(а) можна бачити, що смуга пропускання практично визначається положенням найближчого до уявної осі полюса  Отже, якщо в системі можна здійснити корекцію, яка створить окремий нуль  то для ефективної корекції його необхідно розмістити там же де, і полюс  тобто сумістити полюс  з нулем , рис. 1.3 (б). Суміщення його, наприклад, з полюсом  практично не розширить смуги, а тільки зменшить падіння частотної характеристики у межах від  до . Якщо застосовуючи корекцію можна одержати два нулі –  та  – то ними, як можна бачити з рис. 1.3 (б), необхідно компенсувати два найближчих до уявної осі полюси  та  Компенсація елементами корекції всіх полюсів неможлива, бо призводить до системи з фізично недосяжною необмеженою смугою пропускання.

На рис.1.4(а) показано випадок положення полюсів для оптимальної корекції.

У цьому випадку необхідно, у першу чергу, сумістити нулі з полюсами, найближчими до уявної осі, і, якщо полюси комплексні, тоді і компенсувальні нулі виявляються також комплексними.
 При компенсації полюсів нулями відповідні пари нулів та полюсів у виразі (1.7) скорочуються, і вираз для частотної характеристики спрощується.

Оптимальне положення нулів та полюсів на рис. 1.4(а) відповідає системі мінімально–фазового типу, бо всі особливі точки  розміщені в лівій напівплощині.

Здійснюючи корекцію iз залученням немінімально–фазових ланок, одержимо положення нулів та полюсів, що показані на рис. 1.4(б). У цьому випадку нулі, що корегують характеристику, як і раніше мають однакові з полюсами дійсні та уявні частини, але знак останніх для нулів додатний. Використовуючи такі ланки, можна здобути ідеальну частотну характеристику у широкому діапазоні частот. Фазовий зсув у такій ідеально–коригованій системі лишається залежним від частоти, тому включення подібних ланок у тракт підсилення, не змінюючи його частотних властивостей, дозволяє змінити його фазову характеристику. Такі ланки називають фазовими коректорами.

Розглянемо випадок, коли система має два комлексно–поєднаних полюси, а корекція можлива тільки з використанням одного нуля. У цьому випадку

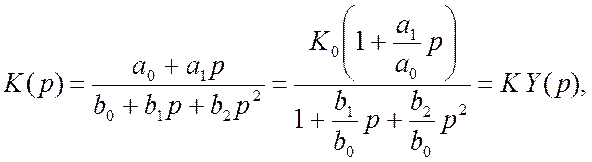
де

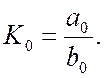
Для спрощення подальших записів пропонується зміна р та введення замість неї змінно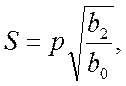ї  тоді

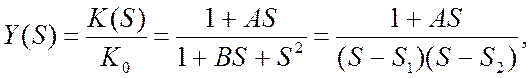
де 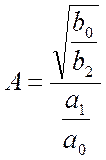,  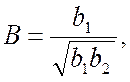a  та  – полюси

Розв'язуючи рівняння  знаходимо полюси  При  полюси комплексно–поєднані. Тоді

де   Модуль коренів  тобто при будь-яких значеннях  полюси лежать на колі з одиничним радіусом, рис. 1.5 (а).

 

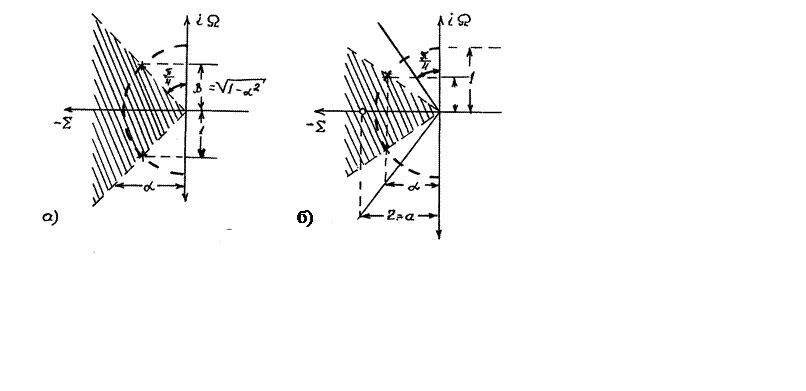Рисунок 1.5 – Зображення полюсів

Модуль частотної характеристики знаходиться після заміни S на

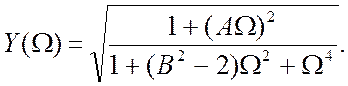
Згідно з умовою Брауде кореція має місце при  або  У цьому випадку може бути отримана частотна характеристика без підіймання з максимальною шириною смуги:

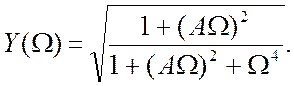
Якщо прирівняти цей вираз до 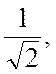 можна знайти максимальну граничну частоту

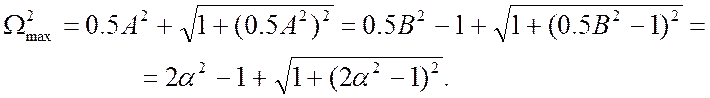
Вона однозначно визначається можливою величиною  при такому положенні нуля 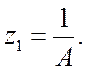 Зв'язок між  та  що відповідає умовам корекції Брауде, має вигляд

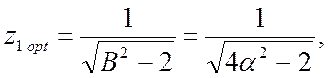
Числові значення  та  наведені у табл. 1.1.

Якщо нуль знаходиться у нескінченності, корекція за Брауде збігається з корекцією за Баттервортом. Обидва полюси при цьому розміщені на колі

Таблиця 1.1

0,707 1,0 0 1,55

0,900 0,900 0,440 1,34

1 0,865 0,500 1,27

1,19 0,82 0,575 1,19

1,55 0,775 0,631 1,11

2,0 0,75 0,663 1,07

5,0 0,715 0,700 1,01

0,707 0,707 1,00

під кутом  і знаходяться один від одного на кутовій відстані  (рис.1.2(б) та рис.1.5(а)).

Якщо їх розташувати праворуч (відносно рис.1.5(а)), то частотна характеристика виявиться вже не максимально плоскою і на ній з'явиться нерівномірність у вигляді підйому. Якщо їх розташувати ліворуч (у межах заштрихованого сектора), то характеристики, не будучи максимально плоскими, лишаться монотонними. Поява кінцевого нуля на дійсній осі зменшує кут розташування полюсів, у межах якого зберігається монотонність частотних характеристик (заштрихований сектор на рис.1.5(б)). Конкретні співвідношення між можливими положеннями полюсів і нулів подані у табл.1.1.