Аналогові та підсилювальні електронні пристрої. Частина 2: Навчальний посібник, страница 15

Вхідний опір імітатора індуктивності зворотно пропорційний опору ЗЗ  і визначається виразом . Якщо  конденсатор ємністю , то вхідний опір – , тобто вхідний опір еквівалентний індуктивності .

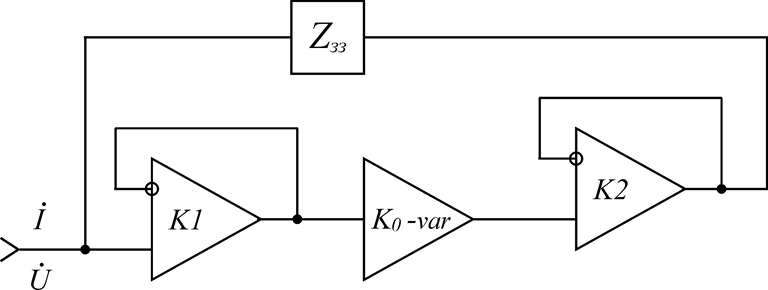
 Рисунок 4.3 – Помножувач ємності

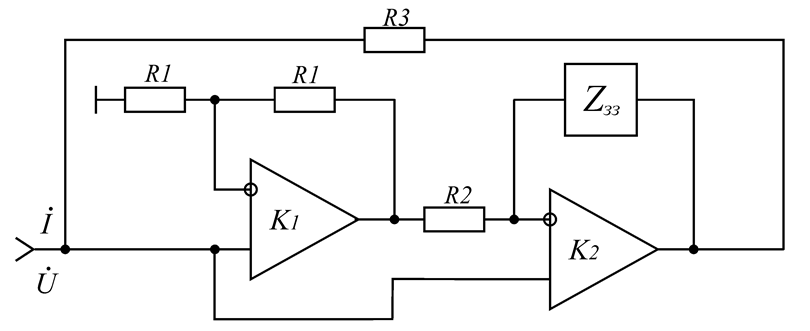
Рисунок 4.4 – Еквівалентна індуктивність

Контрольні завдання та запитання

1.  Яким вимогам повинен відповідати ОП інвертора імпедансу?

2.  Які коефіцієнти підсилення каскадів К1 та К2 помножувача ємності?

3.  Які опори (вхідний, вихідний) повинні бути забезпечені в помножувачі ємності?

5 Активні фільтри

5.1 Загальні відомості про фільтри

При використанні ОП як одного з елементів пристрою з'являється можливість синтезувати характеристику будь–якого LC фільтра без використання котушок індуктивності. Такі фільтри відомі під назвою «активних фільтрів», у зв’язку з наявністю в схемі активного елемента (ОП).

Активні фільтри можна використовувати для реалізації фільтрів НЧ,ВЧ, смугопроникальних і смугозатримувальних, вибираючи тип фільтра у залежності від його властивостей; рівномірності підсилення в смузі пропускання, крутості перехідної ділянки АЧХ або незалежності часу затримки від частоти. Окрім цього можна також побудувати «усепроникаючі фільтри» з плоскою АЧХ, але нестандартною ФЧХ (такі фільтри називають «фазові коректори»), або навпаки фільтри з постійним фазовим зсувом, але довільною АЧХ.

Коефіцієнт передачі фільтра у загальному випадку можна записати у вигляді

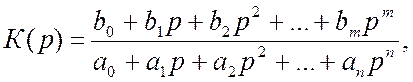                            (5.1)

де – дійсні числа; р – оператор Лапласа, для синусоїдального сигналу .

Порядок фільтра визначається найбільшим степенем оператора р у знаменнику. Якщо відомі корені  чисельника і корені  знаменника, то коефіцієнт передачі можна записати у вигляді

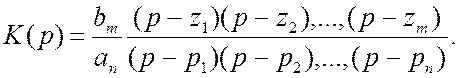                         (5.2)

При  коефіцієнт передачі дорівнює нулю, тому корені  називають нулями. При  коефіцієнт передачі дорівнює нескінченності, тому корені  називають полюсами.

Коефіцієнт передачі фільтра повністю визначається значеннями нулів і полюсів, а також сталим множником

Коефіцієнт передачі фільтра першого порядку

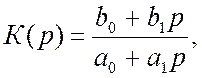                                               (5.3)

де

У відповідності з виразом (5.3) коефіцієнт передачі фільтра НЧ може бути записаний при

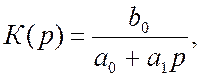
для ФВЧ, при

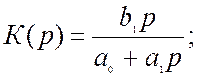
для фазового коректора, при ,

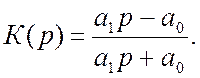
Коефіцієнт передачі фільтра другого порядку

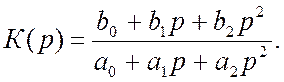                                       (5.4)

Виходячи з виразу (5.4), коефіцієнт передачі відповідних фільтрів можна подати у вигляді:

для ФНЧ, при

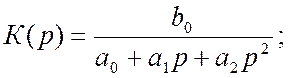
для ФВЧ, при

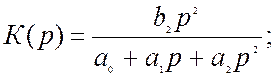
для смугопроникального фільтра, при

для смугозатримувальних фільтрів, при

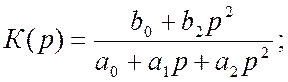
для фазового коректора, при

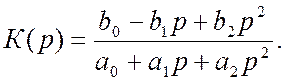
Фільтри другого порядку можна реалізувати, з'єднуючи відповідним чином ланки першого і нульового порядку. Спосіб такої реалізації витікає з можливої форми подання коефіцієнта передачі у вигляді елементарних функцій інтегрування, диференціювання, підсумовування. Оскільки способів подання виразу (5.4) через елементарні функції може бути досить багато, то і число можливих схемних рішень фільтрів другого порядку може бути значним.

На практиці фільтр характеризується трьома основними параметрами: – характеристична частота (зрізу), що характеризує рівень послаблення АЧХ –3 дБ;  модуль коефіцієнта передачі у смузі пропускання; – коефіцієнт згасання коливань.

Смуга пропускання і добротність Q пов'язані з коефіцієнтом згасання співвідношенням

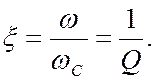
Відомі три найбільш популярні типи активних фільтрів: Баттерворта, (максимально плоска характеристика в смузі пропускання), фільтр Чебишева (найбільш крутий перехід від смуги пропускання до смуги придушення) та фільтр Бесселя (максимально плоска характеристика часу затримки). Будь–який з цих фільтрів можна реалізувати за допомогою різних схем. Всі вони придатні для побудови фільтрів верхніх, нижніх частот і смугових фільтрів.

5.2 Фільтри Баттерворта і Чебишева

Фільтр Баттерворта, як відзначено вище, забезпечує найбільш плоску характеристику в смузі пропускання, що однак досягається за рахунок повільної зміни характеристики у перехідній області, тобто між смугами пропускання і затримки. Він також має погану фазочастотну характеристику, тобто таку, що викликає значні фазові спотворення. Його амплітудно–частотна характеристика задається таким виразом