






В работе железнодорожного транспорта имеют место неравномерные процессы, с которыми необходимо считаться. Например, для определения среднего времени ожидания обработки составов на сортировочной станции может быть использована формула
tож=y2бр(n2вх+n2обр)tобр/2(1-y2), то есть tож=F(n)
А для того, чтобы давать правильную оценку тому или другому варианту технологического, технического решения необходимо учитывать вероятностную оценку того или иного процесса, их совокупности.
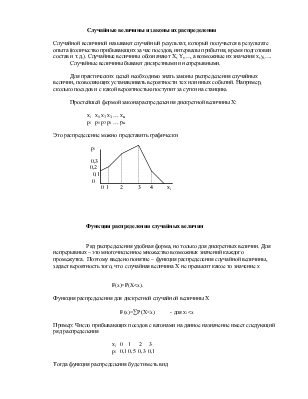
Для этого следует знать законы распределения случайных величин.
Событие – факт, который может произойти , либо не произойти.
Событие может быть достоверным, невозможным, случайным.
События могут быть равновозможными, несовместными, совместными.
События бывают противоположными (А, А).
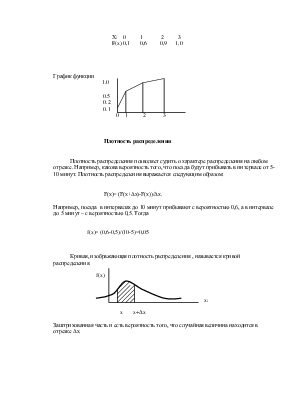
Частота события P*(А)=m/n,
где n – число испытаний,
m – число испытания с появлением события А.
Свойство частоты:
1) 0<P*<1;
2) Частота достоверного события равна 1;
3) Частота невозможного события равна 0;
4) Если в результате опыта может появиться либо событие А, либо В (несовместные события), то частота этих событий (общая) равна сумме этих частот
Р*(А+В)=Р*(А)+Р*(В) - правило сложения частот;
5) Частота появления двух совместных событий равна произведению частоты одного на условную частоту другого
Р*(АВ)=Р*(А)Р*(В/А) – правило умножения частот.
Частоту называют вероятностью события. Аналогично частоте
Р(А)=m/n, 0<P(A)<1/
Теорема сложения вероятностей несовместных событий
Р(А+В)=Р(А)+Р(В).
Для полной группы совместных событий
Р(А)+Р(В)+…+Р(N)=1
Сумма вероятностей противоположных событий
Р(А)+Р(А)=1
или Р(А)=1-Р(А)
или р+q=1.
Для совместных событий вероятность их суммы
Р(А+В)=Р(А)+Р(В)-Р(А,В),
Где Р(А,В) –вероятность их совместного появления.
События бывают зависимые и независимые.
Вероятность произведения или совместного наступления событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие произошло
Р(АВ)=Р(А)Р(В/А).
Следствие: Вероятность произведения независимых событий равна произведению их вероятностей
Р(АВ)=Р(А)Р(В)
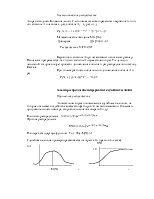
Полная вероятность
Вероятность события А, которое может произойти вместе с одной из гипотез Н1, Н2, …,Нn равна сумме парных произведений вероятностей каждой из этих гипотез на соответствующие им условные вероятности наступления события А
Р(А)=ånЗ(Нi)P(A/Hi).
С помощью данной формулы можно, например, определить вероятность того, что в прибывающем поезде имеются вагоны определенного назначения. В этой задаче гипотезами будут вероятности прибытия поездов с того или иного направления. Каждому направлению будет соответствовать вероятность наличия в этих поездах вагонов рассматриваемого назначения Р(А/Н).
Для определения вероятности того, что в очередном поезде имеются вагоны рассматриваемого назначения (применительно к рассмотренной задаче) можно использовать формулу БЕЙЕСА
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.