Случайные величины и законы их распределения, страница 3

                                         F(x)=P(X<x).

Функция распределения для дискретной случайной величины Х

                                               F(x)=åР(Х<x)           - для х_i <x

Пример: Число прибывающих поездов с вагонами на данное назначение имеет следующий ряд распределения

                                         х_i     0   1      2     3

                                         p_i   0,1 0,5  0,3  0,1

Тогда функция распределения будет иметь вид

                                         Х_i     0          1             2          3

                                         F(x) 0,1       0,6         0,9      1,0

График функции

                                  1.0

 

                                   0.5

                                   0.2

                                   0.1

                                            0    1           2            3

Плотность распределения

            Плотность распределения позволяет судить о характере распределения на любом отрезке. Например, какова вероятность того, что поезда будут прибывать в интервале от 5-10 минут. Плотность распределения выражается следующим образом:

                                   F(x)= (F(x+∆x)-F(x))/∆x.

Например, поезда  в интервалах до 10 минут прибывают с вероятностью 0,6, а в интервале до 5 минут – с вероятностью 0,5. Тогда

                        f(x)= (0,6-0,5)/(10-5)=0,05

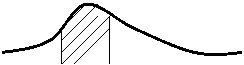
            Кривая, изображающая плотность распределения , называется кривой распределения.

                              f(x)

 

                                                                                                          x_i

                                               x       x+Dx                            

Заштрихованная часть и есть вероятность того, что случайная величина находится в отрезке ∆х.

Числовые характеристики случайных величин

Зная закон распределения случайной величины можно установить с какой вероятностью она появляется в том или ином интервале. Для практических целей бывает достаточным знать некоторые числовые характеристики –математическое ожидание, дисперсию, среднее квадратическое отклонение.

            Математическое ожидание для дискретной величины

М[Х] = х₁р₁₊х₂р₂+…+х_nр_n.

Для непрерывной случайной величины

М[Х]= _а∫^вхf(x)dx.

Пример расчета математического ожидания для величин составов:

х_i     50   51   53   54

р_i      0,1  0,2  0,4  0,3        М[Х]=50*0,1+51*0,2+53*0,4+54*0,3=52,6 вагонов.

МОДА – наиболее вероятное значение случайной величины.

МЕДИАНА – то значение случайной величины, когда равновероятно получение случайной величины большего или меньшего значения.