Случайные величины и законы их распределения, страница 5

                                           Математическое ожидание М[х_i]=np_i

                                                          Дисперсия                            Д[х_i]=np_i(1-p_i)

                                               Распределение ПАСКАЛЯ

Вероятность события А при независимых испытаниях равна р. Испытания прекращаются, как только событие А осуществлено n раз. Тогда число испытаний которое следует провести до появления события n раз распределено по закону Паскаля.

                                           При этом вероятность числа опытов до появления события А n раз

                                               Р(Х₁=х)=(p/(1-p))*С^n-1_x-1*(1-p)^x

                                           Законы распределения непрерывных случайных величин    

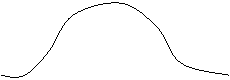
Нормальное распределение

                                           Этим законом хорошо описываются случайные величины, на которые оказывает воздействие множество факторов. Этим законом можно. Описывать продолжительность осмотра, скорости выполнения операций и др.

Плотность распределения    f(x)=(1/sÖ2p)е^{-(х-М(Х))(х-М(Х)/2s*s}

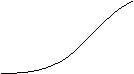
Функция распределения   

                                                           F(X)=(1/2p)_-¥ò^xе^{-(х-М(Х))(х-М(Х)/2ss}dx

Или черех стандартную функцию  F(x)= Ф(х-М(Х)/s)

Случайная величина примерно рассеивается на отрезке 3s (правило 3-х сигм).

                                                                                                   F(X)

f(x)

                                                                                              1.0

 

                                  М[Х]                             x_i                                                                                          x_i

                      Равномерное распределение

 Это распределение в интервале с равной вероятностью

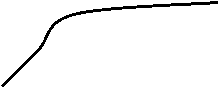
                      Распределение ЭРЛАНГА

Оно получается из Пуассоновского потока путем объединения интервалов: двух, трех и т.д. Поэтому имеют 2-й, 3-й и т.д. порядок (k)

     F_k(t)=((l_kk)^k/(k-1)!)*t^k-1е^-лl_kt

М[T]=k/l    Д[Т]=k/ll

                                                  F(x)

                                                  1.0